Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 13.Problemas - Ex. 6

Um bloco de massa encontra-se em repouso sobre uma cunha de ângulo de inclinação . A cunha, inicialmente em repouso sobre uma mesa horizontal, é colocada em movimento com aceleração de magnitude , que se faz crescer gradualmente(Fig.). Se é o coeficiente de atrito estático entre o bloco e a cunha, para que valor de o bloco começara a deslizar para cima sobre a cunha?

Passo 1

A ideia pra mudar de referencial é basicamente esquecer essa aceleração pra direita e colocar uma aceleração pra esquerda considerando que o sistema estará em equilíbrio. Assim, teremos uma força de módulo atuando na mesma direção, mas em sentido contrário atuando no bloco.

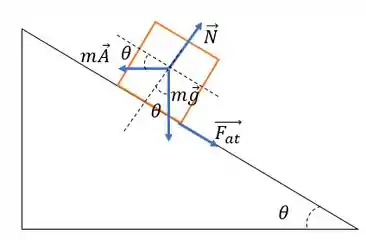
Escrevendo as esquações de Newton:

Onde é a aceleração horizontal

Passo 2

Como , podemos usar a primeira equação do sistema:

Na segunda equação:

Agora basta fazemos . Assim,

Isolando :

Assim o bloco começara a subir para:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco retangular alto e uniforme fica em um plano inclinado, conforme mostrado na Figura 12-45. Um cabo é preso ao topo do bloco para evitar que ele caia no declive. Qual é o ângulo máximo θ para o

Para o cilindro do problema 25, determine uma expressão para a magnitude mínima da força horizontal F → que fará o cilindro rolar sobre o degrau, supondo que ele não deslize na borda.

Uma escada, de massa m e comprimento L , está apoiada contra uma parede sem atrito, formando um ângulo θ com a horizontal. O centro de massa da escada está a uma altura h acima do piso. Uma força F ,

Um homem de 900 N está sentado no topo de uma escada de massa desprezível, colocada sobre um piso sem atrito, como na figura 12-43. Existe um tirante, no meio da escada. O ângulo de abertura é θ = 30

Uma escada homogênea, de comprimento L e massa m , está apoiada contra uma parede vertical sem atrito, formando um ângulo de 60 ° com a horizontal. O coeficiente de atrito estático entre a escada e o