Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 4.Problemas - Ex. 34
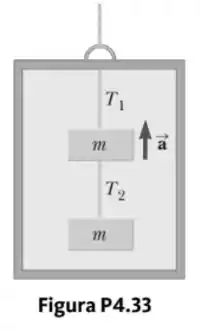
Dois blocos, cada um de massa , estão pendurados no teto de um elevador, como na Figura P4.33. O elevador tem uma aceleração para cima . As cordas têm massa desprezível.
- Encontre as tensões e nas cordas superior e inferior, em termos de , e .
- Compare as duas tensões e determine qual corda se romperá caso a seja suficientemente grande.
- Quais são as tensões se o cabo que sustenta o elevador se romper?
Passo 1
E aiii galera, vamos fazer uma questão aqui?
Vem comigo!
Letra a:
Aplicando a segunda lei de Newton no bloco de baixo:
E para o bloco de cima:
Passo 2
Letra b:
Intuitivamente, a tensão na corda superior é maior à medida que segura as duas massas. Podemos ver que , então a corda de cima quebra primeiro se (a) for suficientemente grande.
Passo 3
Letra c:
Para as tensões, temos:
São iguais.
Resposta
- A corda de cima quebra primeiro se (a) for suficientemente grande.
Exercícios de Livros Relacionados
Um bloco de massa M é amarrado na extremidade inferior de uma corda de massa m e comprimento L . Uma força F → constante é aplicada de baixo para cima na extremidade superior da corda, fazendo com que
Um objeto de 10 kg está sobre uma mesa sem atrito e sujeito a duas forças horizontais, F → 1 e F → 2 de magnitudes F 1 = 20N e F 2 = 30N , como mostrado na Figufra 4-40. Encontre a terceira força hori
Uma lâmpada de 42,6 kg está suspensa por fios, como mostrado na Figura 4-37. O anel tem massa desprezível. A tensão T 1 no fio vertical é (a) 209 N, (b) 418 N, (c) 570 N, (d) 360 N, (e) 730 N.
Uma bola pesando 100 N é mostrada suspensa por um sistema de cordas (Figura 4-39). Quais são as tensões nas três cordas?
Um sinal luminoso de trânsito, de 35,0 kg, é mantido suspenso por dois fios, como na Figura 4-36. (a) Desenhe o diagrama de corpo livre para o sinal e utilize-o para responder qualitativamente à segui