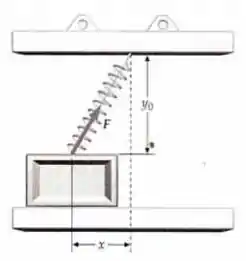
Um bloco de massa m, sobre uma mesa horizontal sem atrito, é preso a urna mola que está fixa ao teto (figura abaixo). A distância vertical entre o topo do bloco e o teto é , e sua posição horizontal é x. Quando o bloco está em x = 0, a mola, cuja constante de força é k, está completamente frouxa. (a) Quanto vale a componente x da força da mola sobre o bloco, como função de x? (b) Mostre que é proporcional a para valores de suficientemente pequenos. (c) Se o bloco é largado do repouso em , com , qual é sua rapidez ao atingir x = 0?
Passo 1
Letra (a)
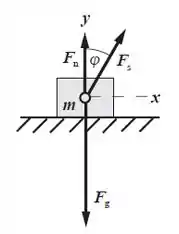
Pra começar, a temos que:
O sinal de menos é porque a componente é restauradora, sempre tentando trazer o bloco de volta para a origem. Além disso, temos:
Então
Passo 2
Agora vamos usar um pouquinho de trigonometria:
Joga lá na força
Agora a gente usa o teorema de Pitágoras:
Joga lá na expressão da força
Passo 3
Letra (b)
Agora a gente vai precisar dar aquela forçada de barra. Vamos lembrar daquela aproximação:
Essa aproximação aí vale quando x é bem pequeno. Vamos voltar para a força:
Passo 4
Como x é bem pequeno, x/y também é:
Joga isso lá na força:
Passo 5
Letra (c)
Vamos usar o teorema do trabalho-energia:
Passo 6
Sabemos que
Passo 7
Joga esse trabalho lá no teorema do trabalho-energia:
Agora a gente isola o :
Resposta
Letra (a):
Letra (b): ver solução para ver que
Letra (c):