Uma bola sólida e uniforme, de e diâmetro de está presa a um suporte vertical livre de atrito por um fio de e massa desprezível (Figura ).

a) Faça um diagrama do corpo livre para a bola e use-a para achar a tensão no fio.

b) Qual é a força que a bola exerce sobre a parede?

a) Esboçando um diagrama do corpo livre do nosso sistema, ficamos com:

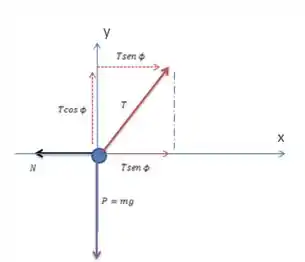
Temos o peso da bolinha, que é dado por e temos a tensão no cabo, que gente decompôs ali bem bonita em relação aos nossos eixos coordenados.

Uma coisa importante é ver que a gente colocou uma força normal ali. Ela é a força que surge do contato entre bola e parede, tá bem?

Queremos a tensão na corda. Olhando para a direção vertical podemos descobrir quanto vale a tensão:

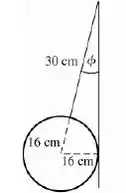
Mas não sabemos o ângulo, e agora?? Calma, se liga só nessa figura aqui pra ajudar a gente:

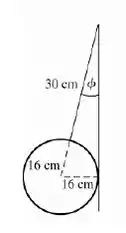
Logo, sabemos os lados desse triângulo! Lembrando que seno é a divisão do cateto oposto pela hipotenusa, sendo assim (olhando a figura), ficamos com:

E calculando o arco seno dessa ângulo, obtemos:

Beleza! Agora sim podemos voltar para nossa força e descobrir :

Então, substituindo os valores, temos a tensão:

b) Show! Agora o problema pede para calcular a força que a bola exerce na parede. Mas que força é essa, pequeno gafanhoto? É de contato!!! Vamos olhar para o diagrama de forças, mas agora na direção horizontal. Assim, temos:

Já conhecemos o ângulo e a tensão! Então substituindo, obtemos o valor da força de contato:

Valeu, galera! Até a próxima! 😉