Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.5 - Ex. 35
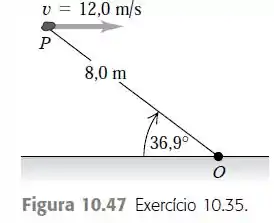
Uma pedra de 2,0 kg possui uma velocidade horizontal com módulo de 12,0 m/s quando está no ponto P na Figura 10.47. a) Nesse instante, qual é o módulo, a direção e o sentido do seu momento angular em relação ao ponto O? b) Caso a única força que atue sobre a pedra
seja seu peso, qual é a taxa de variação (módulo, direção e sentido) do momento angular nesse instante?
Passo 1
- Nós vamos usar a equação:
- Pela equação para uma partícula sob ação da força resultante , a taxa de mudança do momento angular da rocha é igual à torque da força total que atua sobre ele.
Mas primeiro, vamos considerar o seguinte diagrama:
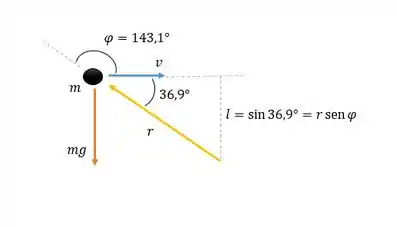
E separar os dados:
E então,
Para encontrar a direção de aplique a regra da direita girando na direção de empurrando-o com o dedos da sua mão direita. Seu polegar aponta para a página, na direção de .
Passo 2
Para encontrar a direção de e, portanto, de aplique a regra da direita girando na direção da força gravitacional empurrando-a com os dedos da mão direita. Seu polegar aponta para fora da página, na direção de .