Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 29.Exercício - Ex. 30

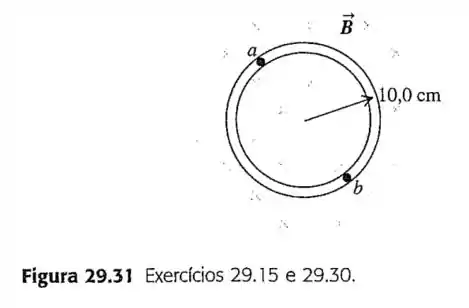
30- O campo magnético B → em todos os pontos do círculo no interior do anel indicado na Figura 29.31 possui um módulo inicial igual a 0.750   T . (O círculo poderia representar aproximadamente o espaço no interior de um solenóide longo.) O campo magnético está direcionado para o interior da figura e diminui com uma taxa igual a - 0.0350   T / s .

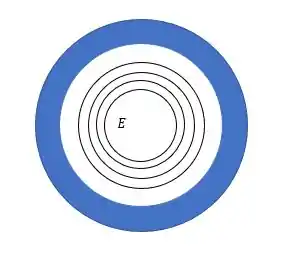
( a ) Qual é a forma das linhas do campo elétrico induzido, indicado na Figura 29.31 , no interior desse círculo?

( b ) Qual é o módulo, a direção e o sentido desse campo em qualquer ponto do anel condutor com raio igual a 0.100   m ?

( c ) Qual é a corrente que circula no anel, sabendo que sua resistência é de 4.0   Ω ?

( d ) Qual é a fem entre os pontos a e b do anel?

( e ) Se o anel for cortado em um certo ponto e as extremidades forem separadas ligeiramente, qual será a fem entre essas extremidades?

Passo 1

A figura 29.31 é a que está na página 307 (pelo menos na quinta edição desse livro). A forma (superfície) da linha do campo elétrico é de círculos que estão concêntricos dentro do anel, de forma que temos.

Já o vetor como pode ser visto na página 304 (da quinta edição) são retas tangentes a esses círculos, para um raio de anel de 0.1   m teremos:

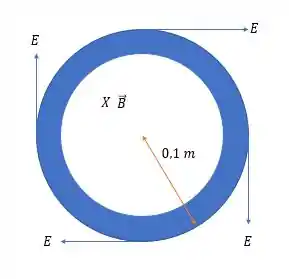
Esse sentido faz sentido pois pela Lei de Faraday o vetor campo elétrico tem que ficar paralelo ao vetor d l ∮ E ⋅ d l = - d ϕ / d t   , e como o fluxo é negativo para um campo magnético entrando então E é positivo e sentido horário.

Pela lei de Faraday a intensidade desse campo elétrico induzido será de:

E ⋅ 2 π 0.1 = - d B d t π r 2

Já que é um anel de espessura fina.

Onde d B d t = - 0.035   T / s

E = 0.1 × 0.035 2 = 1.75 × 10 - 3 V m

Passo 2

A tensão induzida pode ser encontrada pelo campo elétrico induzido e que será de:

ϵ = E l = 1.75 × 10 - 3 × 2 π × 0.1 = 1.1 × 10 - 3   V

Logo a corrente será de:

I = ϵ R = 1.1 × 10 - 3 4 = 2.75 × 10 - 4   A

Passo 3

Os pontos a e b equivalem a meio círculo, logo a fem será de:

ϵ = E π r = 1.75 × 10 - 3 × π × 0.1 = 5.5 × 10 - 4   V

Fazendo o corte no anel, e quisermos a fem nessa linha.

ϵ = E 2 π r = 1.1 × 10 - 3   V

Pois nesse caso teremos o comprimento do círculo todo que vale 2 π r , tal como calculado na letra c (passo 2)

Resposta

a )   C í r c u l o s   c o n c e n t r i c o s   d e n t r o   d o   a n e l

b )   1.75 × 10 - 3 V m

c )   2.75 × 10 - 4   A  

d )   5.5 × 10 - 4   V

e )   1.1 × 10 - 3   V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os supercondutores são diamagnéticos perfeitos, ou seja, sua suscetibilidade magnética é χ m = - 1 . Mostre que independentemente das correntes elétricas existentes na vizinhança do supercondutor, o c
Um cilindro feito de alumínio, com raio e comprimento iguais a 5,0c m , está sob o efeito de um campo magnético homogêneo de 1,5T , alinhado com o eixo do cilindro. Sabendo-se que a suscetibilidade ma
Utilizando o resultado obtido no 25.1P e os dados da Tabela 25.1, calcule a suscetibilidade magnética do Bi, Pb, H 2 O , Al, e O 2 ( 90K ), sabendo que as densidades de massa desses materiais, em g /
A Figura 25.8 mostra dois blocos imantados de Alnico V, ambos com volume de 250c m 3 . Utilizando a aproximação de dipolo para a interação entre os dois blocos, calcule a força de atração entre eles.
Calcule o torque de um bloco imantado de Alnico V com volume de 1000c m 3 , submetido a um campo magnético de 0,100T perpendicular ao seu dipolo.