Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 86
Uma bola de está presa a um poste vertical por uma corda de . Assuma que o raio da bola é desprezível. Se a bola se move em um círculo horizontal com a corda fazendo um ângulo de com a vertical, (a) qual é a tensão na corda? (b) Qual é a rapidez da bola?
Passo 1
Vamos fazer um esquema para representar a situação:
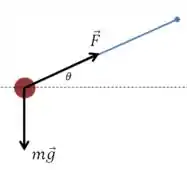
Queremos que haja equilíbrio na direção vertical:
E na direção horizontal precisa haver uma resultante centrípeta:
Essas são as duas equações que vamos usar para resolver o problema. Com os valores dados no enunciado, já podemos usar a primeira para calcular :
Perceba que o enunciado deu o ângulo que a corda forma com a horizontal, mas nós definimos o da forma como está no desenho:
Passo 2
(b) E agora vamos usar a segunda equação para encontrar a rapidez da bola:
Cuidado na hora de substituir , ele não é igual ao comprimento da corda, ele é a projeção de na horizontal:
Resposta
(a) .
(b) .