Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 87
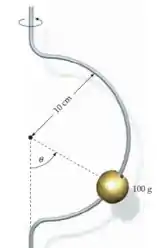
Uma pequena bola com massa de desliza sem atrito por um fio em semicírculo com raio de que roda em torno de um eixo vertical a uma taxa de revoluções por segundo. Encontre o valor de para o qual a bola se mantém estacionária em relação ao fio que roda.
Passo 1
Vamos fazer um esquema simples da situação:
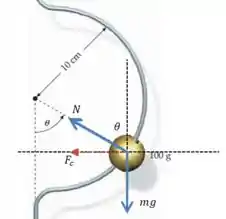
A seta vermelha não é uma força “real”, é apenas uma representação da direção da força centrípeta.
Não queremos que a bola deslize ao longo do arco, mas ela vai girar junto com ele em torno do eixo vertical, então teremos uma resultante centrípeta na direção de :
E queremos que haja equilíbrio na direção vertical, ou seja:
Então ficamos com o seguinte sistema:
Passo 2
Nosso objetivo é encontrar o valor de , vamos começar dividindo a primeira equação pela segunda:
Não esqueça que e se referem ao movimento do arco em torno do eixo vertical, e o raio vai depender do ângulo e do comprimento do raio do arco, ou seja:
Precisamos reescrever pela sua definição para um movimento circular:
E então:
E lembrando que :
Passo 3
Como o arco completa duas revoluções a cada segundo, podemos deduzir que ele leva meio segundo para completar cada revolução, então :
Resposta
A bola se mantém estacionária em relação ao fio quando .