Uma bola de é amarrada à extremidade de um fio de de comprimento e balançada de modo a perfazer um círculo vertical.
a) Por um círculo completo, com início em qualquer ponto, calcule o trabalho total realizado sobre a bola
i) pela tensão no fio; e
ii) pela gravidade.
b) Repita o item (a) para o movimento ao longo de um semicírculo, do ponto mais baixo ao ponto mais alto da trajetória.
Passo 1
Opa, bora resolver esse problema! Aqui temos uma amarrada na ponta de um fio de de comprimento e balançada de modo a perfazer um círculo vertical.
Se liga nesse esqueminha:
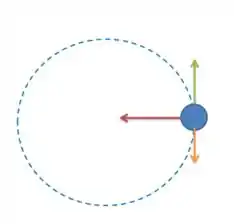
Vamos calcular o trabalho total realizado pela bola pra rodar um círculo completo!
Vamos supor que a bola esteja girando no sentido anti-horário. O vetor deslocamento está representado em verde, a força tensora está representada pelo vetor em vermelho e a força peso, pelo vetor laranja. A tensão no fio, em qualquer ponto da trajetória vai ser perpendicular ao deslocamento, então o ângulo formado entre eles é .
A força peso é vertical para baixo em todos os pontos e forma um ângulo de com o deslocamento. Em uma volta completa, a bola não tem deslocamento, pois retorna ao seu ponto inicial.
Com isso podemos calcular os trabalhos dessas forças:
Primeiro da força tensora. A força tensora é igual a força centrípeta, e não temos a velocidade para poder calcular ela. Mas isso não importa, pois lembra que essa força forma um ângulo de com o deslocamento, então ela não realiza trabalho. .
Agora a força peso. A força peso força um ângulo de com o deslocamento e vale , mas uma volta completa tem o deslocamento igual a zero, então a força peso também não realiza trabalho. .
Passo 2
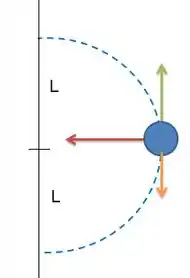
A força de tensão (em vermelho) é sempre perpendicular ao deslocamento (em verde). E a força peso (em laranja) é vertical para baixo, contrária ao sentido do deslocamento. Assim podemos calcular os trabalhos que o problema pede:
Da mesma forma que no item , a tensão é perpendicular ao deslocamento e não realiza trabalho. Assim .
Agora o trabalho realizado da força peso. O deslocamento vertical foi e a força peso faz um ângulo de com o deslocamento, então o trabalho vai ser:
Certo? Vamos pra próxima?