Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 6.Problemas - Ex. 45
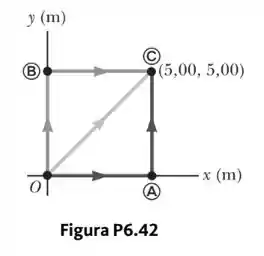
Um corpo se move no plano na Figura P6.42 e está sujeito a uma força de atrito de , sempre agindo na direção oposta à velocidade do corpo. Calcule o trabalho que deve realizar para deslizar o corpo com velocidade escalar constante contra a força de atrito quando ele se move ao longo
- do caminho mais escuro O a A seguido por um caminho cinza escuro de retorno a O,
- o caminho mais escuro de O a C seguido por um caminho cinza claro de retorno a O, e
- o caminho cinza claro de O e C seguido por um caminho cinza claro de retorno a O.
- Cada uma de suas três respostas deve ser diferente de zero. Qual é o significado dessa observação?
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer mais uma questãozinha aqui?
Vem comigo!
Ao longo de cada etapa do movimento, para superar o atrito, você deve empurrar com uma força de 3.00 N na direção do percurso ao longo do caminho, portanto, na expressão para trabalho, .
Letra a:
Passo 2
Letra b:
A distância CO é:
Passo 3
Letra c:
Passo 4
Letra d:
O atrito é uma força não conservadora.
Resposta
- O atrito é uma força não conservadora.
Exercícios de Livros Relacionados
Uma forca F → = 2,0N x 2 i ^ é aplicada sobre uma partícula inicialmente em repouso no plano xy. Encontre o trabalho realizado por esta força sobre a partícula e a rapidez final da partícula, quando e
Uma força atuando sobre uma partícula de 2,0 kg do plano xy, nas coordenadas (x, y), é dada por F → = - b / r 3 x i ^ + y j ^ , onde b é uma constante positiva e r é a distância da partícula à origem.
Uma força horizontal única, com a orientação de +x, atua sobre um carrinho de massa m. O carrinho parte do repouso em x = 0, e sua rapidez cresce com x como v = Cx, onde C é uma constante. (a) Encontr
Uma força atuando sobre uma partícula do plano xy, nas coordenadas (x, y), é dada por F → = F 0 r y i ^ - x j ^ onde F 0 é uma constante positiva e r é a distância dapartícula à origem. (a) Mostre que
Um bloco de massa m, sobre uma mesa horizontal sem atrito, é preso a urna mola que está fixa ao teto (figura abaixo). A distância vertical entre o topo do bloco e o teto é y 0 , e sua posição horizont