Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 10.Exercícios e Problemas - Ex. 56
56. Uma bola de é disparada horizontalmente, com velocidade , contra uma bola de que se encontra em repouso, suspensa por um barbante com de comprimento. As bolas sofrem uma colisão frontal perfeitamente elástica, após a qual a bola de oscila até um ângulo máximo . Quanto vale ?
Passo 1
Nosso passo inicial é fazer uma figura do nosso problema que tornará muito mais fácil o seu entendimento.
Para simplificar a resolução do problema vamos colocar a origem do sistema quando a bola está pendurada imóvel
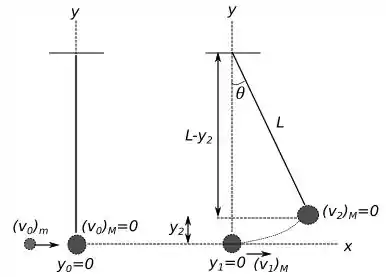
Como podemos ver na figura esse problema pode ser dividido em duas partes. Primeiro, temos uma colisão elástica entre a bola de e a de . Segundo, a bola começa a oscilar como um pêndulo.
Para resolver o problema iremos fazer uso da conservação de energia e da conservação de momento já que ocorre a colisão perfeitamente elástica.
Então, vamos começar.
Passo 2
A primeira parte do problema vamos fazer da seguinte forma:
Quando o livro fala de colisão elástica nesse capítulo ele faz a junção da conservação de energia e de momento em uma colisão perfeitamente elástica com uma bola inicialmente parada que resulta nas equações . Nossa colisão é perfeitamente elástica então podemos utilizá-la de modo que temos:
Substituindo o que temos:
Passo 3
Agora, nessa segunda parte do problema, precisamos pensar bastante na conservação de energia pois a soma da energia potencial gravitacional e da energia cinética é conservada a medida que a bola de inicia seu movimento após a colisão, ou seja:
Quando a bola atinge sua altura máxima ela para e faz o retorno então nesse instante . Nós temos o comprimento do barbante então a altura que alcançará será dada por .
Substituindo essas e outras informações que temos na equação da conservação de energia temos:
Ou seja:
E é esse o resultado do nosso exercício.
Resposta