Uma bola de argila de é arremessada para a direita (sentido positivo do eixo x), a , em direção a outra bola de argila de e em repouso. As bolas de argila colidem e se grudam. Chame de S a este sistema de referência.
a. Qual é o momentum total no referencial S?
b. Qual é a velocidade de um sistema de referência em relação ao qual o momentum total seja nulo?
c. Após a colisão, qual é a velocidade da bola de argila resultante de no referencial S’? Esta questão requer apenas raciocínio, e não cálculos.
d. Use sua resposta ao item anterior e a transformação de Galileu para velocidades a fim de determinar a velocidade pós-colisão da bola de de argila no referencial S.
Passo 1
Desenhando o sistema das duas bolas de argila nós teremos:
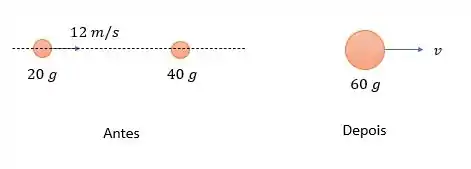
Somando a quantidade movimento que há antes das bolas se colidirem, nós teremos:
E essa é a quantidade de movimento total que age no referencial dado.
Passo 2
E para que tenhamos um sistema de referência cujo momento linear seja nulo nós devemos ter o seguinte:
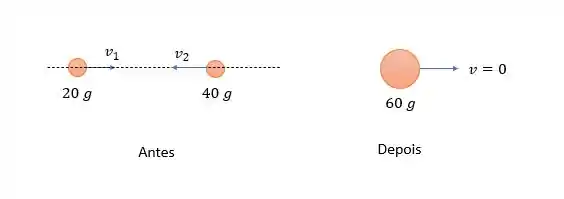
E a soma do momento linear das duas bolas serão de:
E para que tenhamos um sistema como esse imagine que essa velocidade tem sentido para esquerda em relação ao sistema do passo anterior, fazendo com que as velocidades das bolinhas possam ser calculados da seguinte maneira:
Pois é negativa no eixo , portanto no sentido de .
E como então:
É como se o sistema referencial todo fosse acelerado para a esquerda.
E como o momento linear é nulo então a velocidade quando as duas bolas se colidirem é nulo. Pois:
Passo 3
Utilizando a equação da transformação nós temos que a velocidade da bola de argila no referencial seria de:
Isso é válido pela própria conservação de momento linear nesse sistema que nos diz que: