Um caminhão de trafega a em direção ao leste quando, em um cruzamento, sofre duas colisões simultaneamente, uma pelo lado e outra por trás. (Algumas pessoas têm muita sorte!) Um dos carros envolvidos é pequeno, com massa de , e desloca-se para norte a . O outro é um carro médio de que trafega para leste a . Os três veículos ficam presos uns aos outros e derrapam como um só corpo. Qual é o módulo e qual é a orientação da velocidade comum dos veículos logo após a colisão?

Representando todos os automóveis em uma figura só nós teremos:

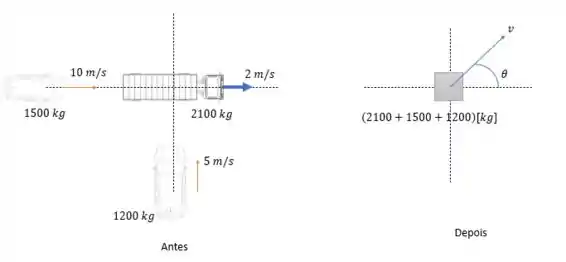
Aplicando a conservação de momento linear no sistema nós teremos:

Igualando os termos com temos:

E igualando os termos em :