Uma bola de bilhar é tacada em direção leste a . Uma segunda bola, idêntica à outra, recebe uma tacada e sai em direção oeste a . Elas chocam-se de raspão, e não, frontalmente, desviando em a segunda bola e mandando-a em direção norte a Quanto vale o módulo e qual é a orientação do movimento da primeira bola após a colisão? Represente a orientação como um ângulo a sudeste.
Passo 1
Melhor caminho para questão de choque entre corpos é desenhar os diagramas antes e depois do choque. E vamos representar as duas bolas de sinuca antes do choque.
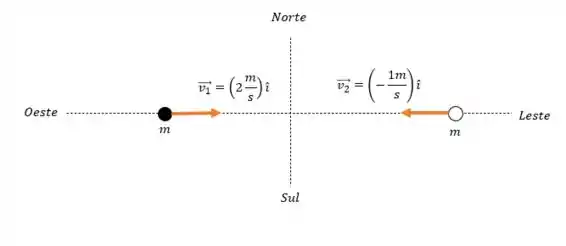
Aqui podemos ver que as duas bolas tem a mesma massa e a bola branca está percorrendo em uma velocidade para trás no sentido . A quantidade de movimento inicial será dada por:
Lembrando que é a direção unitária no eixo e será positivo para leste e negativo para oeste. E será a direção unitária no eixo e será positivo para norte e negativo para sul.
Passo 2
Depois do choque, a bola branca vai na direção norte (com uma velocidade ) e a bola preta segue uma orientação entre e o sul e leste (mais conhecido como sudeste), formando um diagrama igual a:
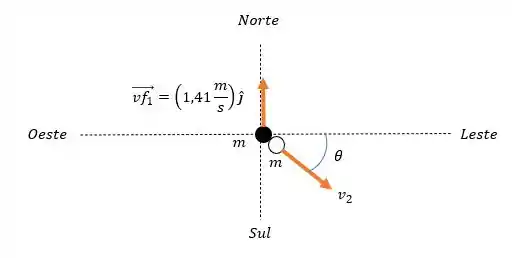
Dessa forma a quantidade de movimento final será dada por:
Onde é a velocidade total da bola branca e sua orientação para o eixo horizontal.
Passo 3
E a conservação do momento linear nos diz que:
Então:
Igualando com nos dois lados da equação nós teremos:
E igualando nos dois lados da equação nós teremos:
Nessa última equação teremos:
Nós temos um valor para e então podemos dividir um pelo outro:
Nos dando:
Logo: