Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 9.Exercícios e Problemas - Ex. 48
Dois blocos de madeira de cada um estão a de distância mútua, sobre uma mesa desprovida de atrito. Uma bala de é disparada a contra os blocos. Ela atravessa inteiramente o primeiro deles e depois fica incrustada no segundo. Imediatamente após a bala tê-lo atravessado, o primeiro bloco se move a . Quanto vale a velocidade do segundo bloco após a bala ter parado dentro dele?
Passo 1
Considerando apenas o sistema da bala e do primeiro bloco nós teremos:
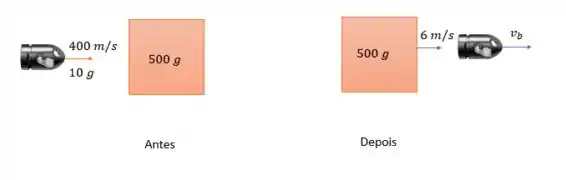
Pois mesmo que o bloco se movimente durante a trajetória da bala dentro dele o momento linear do sistema se conserva. Até mesmo por que o piso onde o bloco se apoia não tem atrito. Dessa forma pela conservação do momento linear teremos a velocidade da bala após a saída do bloco igual a:
Fazendo essa conta teremos a velocidade da bala igual a:
Passo 2
Agora essa bala com velocidade de encontrará o segundo bloco.
E como a bala fica presa no segundo bloco então a massa do sistema passa a ser de e a conservação do momento linear fica:
Então a massa do bloco exatamente no momento em que a bala entra no bloco será de .