Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 12.Problemas - Ex. 3

Calcule o momento de inércia de uma lamina homogênea de massa M em forma de anel circular de raio interno r 1 e raio externo r 2 , (a) Em relação a um eixo perpendicular ao plano do anel, passadno pelo seu centro. (b) Em relação a um diâmetro do anel. Verifique o resultado, nos casos limites de um disco e de um aro circular.

Passo 1

(a) Considerando o anel uniforme, podemos usar a densidade superficial, olhá só:

d m = σ d A

σ = M A = M π r 2 2 - π r 1 2

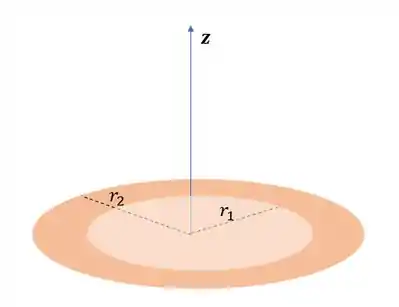
O termo d A , será o seguinte:

d A = d π r 2 = 2 π r d r

Passo 2

Com relação ao eixo passando pelo centro, temos:

I = ∫ r 1 r 2 r 2 d m

Onde r é a distância do centro a um ponto

Logo,

I = ∫ r 1 r 2 r 2 ⋅ M π r 2 2 - π r 1 2 ⋅ 2 π r d r

Arrumando as coisas, temos:

I = 2 M r 2 2 - r 1 2 ⋅ ∫ r 1 r 2 r 3 d r

Integrando, temos:

I = 2 M r 2 2 - r 1 2 ⋅ r 4 4 | r 1 r 2 = 2 M r 2 2 - r 1 2 ⋅ r 2 4 - r 1 4 4

Isto é,

I = M ⋅ r 2 2 + r 1 2 2

Passo 3

Para um eixo passando pelo diâmetro, temos:

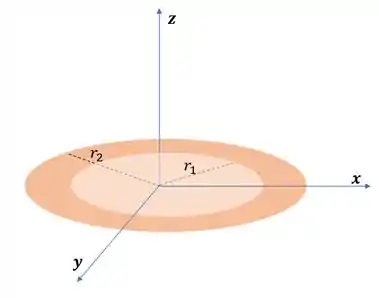
Do problema 1:

I z = I x + I y

Por simetria

I z = 2 I x

No item (a), vimos que

I z = M ⋅ r 2 2 + r 1 2 2 → I x = M ⋅ r 2 2 + r 1 2 4

Verificando os resultado:

  1. Para um aro circular r 1 = r 2 = R , logo:

    2. I c e n t r o = M R 2

    I d i a m e t r o = 2 M R 2

  2. Para um disco r 1 = 0 e r 2 = R , logo:

I c e n t r o = M R 2 4

I d i a m e t r o = M R 2 2

Resposta

  1. I = M ⋅ r 2 2 + r 1 2 2
  2. I = M ⋅ r 2 2 + r 1 2 4
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o seu momento de inércia em relação a um eixo vertical que passa pelo centro do seu corpo, tanto quando você está de pé com seus braços junto ao corpo, quanto quando você está de pé com seus
Determine o momento de inércia de uma esfera maciça e uniforme de massa M e raio R em relação a um eixo tangente à sua superfície.
Duas massas pontuais, m 1 e m 2 , estão separadas por uma barra sem massa de comprimento L . (a) Escreva uma expressão para o momento de inércia I em relação a um eixo perpendicular à barra, que passa
Uma roda de vagão de 1,00 m de diâmetro consiste em um aro fino de 8,00 k g de massa e de 6 raios, cada um com 1,20 k g de massa. Determine o momento de inércia da roda de vagão em relação ao seu eixo
Uma placa retangular uniforme tem massa m e lados de comprimentos a e b . (a) Mostre, por integração, que o momento de inércia da placa em relação a um eixo perpendicular passando por um dos vértices