Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 18

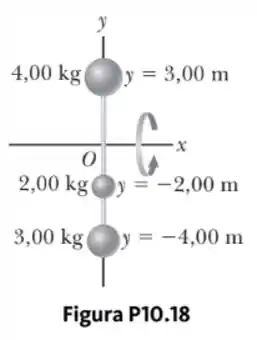
Barras rígidas de massas desprezíveis localizadas ao longo do eixo y conectam três partículas (Fig.P10.18). O sistema gira no eixo x   com velocidade angular de 2,00   r a d / s . Encontre

  1. o momento de inércia em torno do eixo x ,
  2. a energia cinética rotacional total avaliada a partir de 1 2   I w 2 ,
  3. a velocidade tangencial de cada partícula, e
  4. a energia cinética total calculada a partir de ∑ 1 2 m i v i 2 .
  5. Compare as respostas para a energia cinética nas partes (b) e (d).

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

m 1 = 4.00 k g , r 1 = y 1 = 3.00 m m 2 = 2.00 k g , r 2 = y 2 = 2.00 m m 3 = 3.00 k g , r 3 = y 3 = 4.00 m ω = 2.00 r a d / s   n o   e i x o   x

Passo 2

Letra a:

I x = m 1 r 1 2 + m 2 r 2 2 + m 3 r 3 2 I x = ( 4.00 k g ) ( 3.00 m ) 2 + ( 2.00 k g ) ( 2.00 m ) 2 + ( 3.00 k g ) ( 4.00 m ) 2

= 92.0 k g ⋅ m 2

Passo 3

Letra b:

K R = 1 2 I x ω 2 = 1 2 92.0 k g ⋅ m 2 ( 2.00 m ) 2 = 184 J

Passo 4

Letra c:

v 1 = r 1 ω = ( 3.00 m ) ( 2.00 r a d / s ) = 6.00 m / s v 2 = r 2 ω = ( 2.00 m ) ( 2.00 r a d / s ) = 4.00 m / s v 3 = r 3 ω = ( 4.00 m ) ( 2.00 r a d / s ) = 8.00 m / s

Passo 5

Letra d:

K 1 = 1 2 m 1 v 1 2 = 1 2 ( 4.00 k g ) ( 6.00 m / s ) 2 = 72.0 J K 2 = 1 2 m 2 v 2 2 = 1 2 ( 2.00 k g ) ( 4.00 m / s ) 2 = 16.0 J K 3 = 1 2 m 3 v 3 2 = 1 2 ( 3.00 k g ) ( 8.00 m / s ) 2 = 96.0 J K = K 1 + K 2 + K 3 = 72.0 J + 16.0 J + 96.0 J = 184 J = 1 2 I x ω 2

Passo 6

Letra e:

As energias cinéticas calculadas nas partes (b) e (d) são iguais.

Energia cinética rotacional de um objeto girando em torno de um eixo fixo pode ser vista como a energia cinética translacional total das partículas movendo-se em caminhos circulares.

Resposta

  1. 92.0 k g ⋅ m 2
  2. 184 J
  3. 6.00 m s , 4.00 m s , 8.00 m s
  4. 184 J
  5. As energias cinéticas calculadas nas partes (b) e (d) são iguais
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

9.38 Uma batuta consiste em um fino cilindro metálico de massa M e comprimento L. Cada extremidade possui uma tampa de borracha de massa m, e cada tampa pode ser tratada com precisão como uma partícul
9.39 Uma roda de carroça é feita como indicado na Figura 9.30 . O raio da roda é igual a 0,300 m e o aro possui massa igual a 1,40k g . Cada um dos seus oito raios, distribuídos ao longo de diâmetros,
9.37 Uma barra uniforme possui duas pequenas bolas coladas às suas extremidades. A barra possui 2,0m de comprimento e massa de 4,0k g , enquanto as bolas possuem 0,500k g cada uma e podem ser tratadas
Pequenos blocos, todos com a mesma massa m , estão presos às extremidades e ao centro de uma barra leve de comprimento igual a L . Calcule o momento de inércia do sistema em relação a um eixo perpendi
9.35 Calcule o momento de inércia em relação a cada um dos seguintes objetos uniformes em relação aos eixos indicados. Se necessário, use as fórmulas da Tabela 9.2. a) Uma barra delgada de 2,50 kg e 7