Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 82
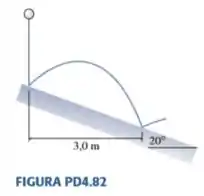
Uma bola de borracha é solta e cai sobre uma rampa inclinada em , como mostra a FIGURA PD4.82. O ricocheteio da bola obedece à “lei da reflexão”, ou seja, a bola deixa a superfície de impacto formando com ela o mesmo ângulo com que dela se aproximou. O local onde a bola ricocheteia pela segunda vez situa-se à direita do local do primeiro ricocheteio. Qual é a rapidez da bola após seu primeiro ricocheteio?
Passo 1
Vamos lá!
Nessa questão, temos uma bolinha que cai verticalmente na direção de uma rampa inclinada, ricocheteia e então é lançada para frente. Fazendo um diagrama do que tá rolando, teríamos algo assim:
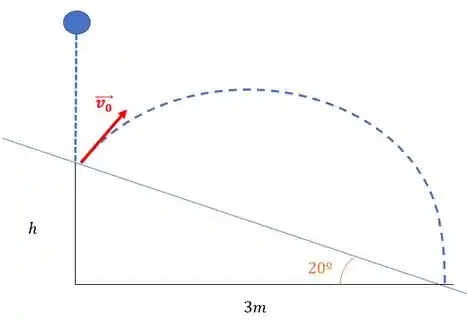
Olhando para esse desenho, dá para perceber que estamos de cara com um lançamento oblíquo. Nesse nosso lançamento, a bolinha é lançada de uma altura , e chega ao “solo” após percorrer um alcance horizontal de 3m. Show! Ah e já podemos definir qual o valor dessa altura , olhando para esse triângulo que foi formado.
Mas a questão quer saber qual o valor do módulo dessa velocidade inicial da bolinha após ricochetear.
Para encontrar essa velocidade, precisamos saber com que ângulo a bolinha ricocheteia e para isso vamos usar essa tal “lei da reflexão” que o enunciado trouxe.
Passo 2
Vamos olhar para o instante em que a bolinha ricocheteia:
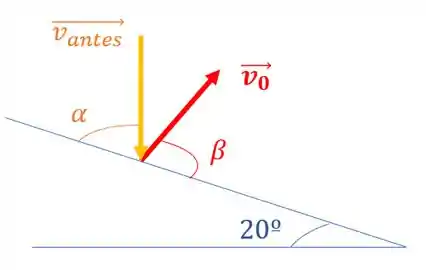
A “lei da reflexão” nos diz que o ângulo com que o objeto bate, é o mesmo com que ele rebate (em resumo, é isso rs). No nosso caso, isso nos diz que
E reparando bem, nós podemos encontrar esse , pois ele é o complemento de 20º que é o ângulo da rampa.
Mas temos que tomar cuidado!!!
Repara que esse ângulo , é o ângulo da velocidade inicial com a rampa! Mas o que a gente precisa de verdade, é o ângulo entre a velocidade inicial e a horizontal, certo??
No desenho acima, o ângulo que realmente queremos é o ângulo . E podemos encontra-lo, pois a soma dele com os é igual ao ângulo de que já tínhamos achado.
Agora que a gente sabe o ângulo da velocidade inicial, bora resolver esse lançamento oblíquo e fechar essa questão!
Passo 3
Com os valores que encontramos nos passos seguintes, temos o seguinte lançamento
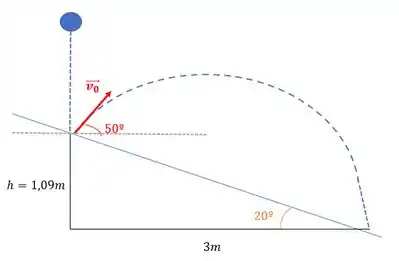
Como todo lançamento oblíquo, vamos trabalhar em dois eixos, o eixo X (Movimento Uniforme) e o eixo Y (Movimento Uniformemente Variado). Para isso, vamos decompor nossa velocidade inicial:
(Repara que a velocidade em x, é constante ao longo de todo o movimento!)
Continuando...
Vamos usar a equação do Movimento Uniforme para o eixo X:
Coloquei o tempo final em evidência, para usa-lo depois na equação do eixo Y, que vai ser a seguinte equação do Movimento Uniformemente Variável:
Se liga que ali em cima, a nossa altura final é igual a 0, enquanto a altura inicial é igual a 1,09. Não confunda um com o outro!
Substituindo o tempo, ficamos com:
Simplificando e usando que