Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 39
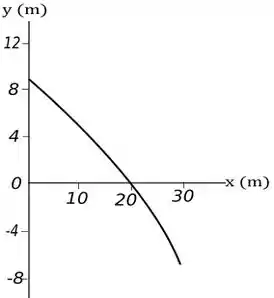
39. Uma partícula parte do repouso em e move-se no plano com a velocidade representada na FIGURA P4.39. A partícula passa por dentro de uma argola de arame localizada em , e depois segue em frente.
- Em que instante a partícula passa através da argola?
- Qual é o valor de , o componente da velocidade da partícula em ?
- Determine e plote a trajetória da partícula.
Passo 1
Então galera para o item temos que pensar no seguinte, a argola está localizada no eixo , então para achar quanto tempo a partícula levou para chegar na argola temos que considerar o movimento da partícula em relação ao eixo .
Para encontrar esse tempo precisamos saber qual a distância percorrida pela partícula nos primeiros onde temos uma velocidade variável em .
Podemos encontrar essa distância lembrando que a posição é igual a área do gráfico da velocidade (nesse caso entre até ).
Depois é só diminuir essa posição que encontramos da posição da argola e depois encontrar quanto tempo leva para partícula percorrer essa distância sabendo que depois de a velocidade é constante e igual a .
Para o item precisamos encontrar para isso vamos usar a seguinte equação:
A velocidade inicial e os tempos nós já conhecemos, falta saber quem é , para isso podemos usar a seguinte equação:
Onde podemos considerar a posição final igual a zero que é o caso do item (já que a argola se encontrava no eixo , logo ) então o valor de que vamos usar é o que vamos encontrar em .
Depois para plotar a trajetória pedida em temos que usar as informações do enunciado de que a partícula está em movimento tanto em quanto em .
Passo 2
Vamos então começar a resolver o que é pedido em . Primeiro vamos encontrar a distância percorrida pela partícula até .
Como falei no passo essa distância é iguala a área do gráfico de até , que é um triângulo, assim temos que:
Substituindo com as informações do gráfico temos:
Então ainda falta a partícula percorrer até a argola. Vamos encontrar quanto tempo ela leva para percorrer essa distância com uma velocidade de , temos o seguinte:
Substituindo com o que sabemos temos:
Então a partícula levou no total para chegar na argola.
Passo 3
Agora vamos partir para o item , mas primeiro precisamos encontrar , então como discutimos no passo , temos:
Onde vamos usar pois assim temos , temos então:
Então temos que:
Passo 4
Agora que temos a aceleração podemos encontrar a velocidade , temos o seguinte:
Substituindo com o que sabemos temos:
Passo 5
Olhando o que o enunciado nos fornece de informação e o que encontramos temos a seguinte trajetória:
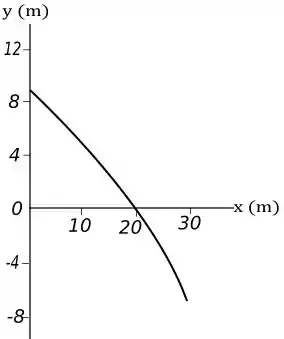
Resposta
