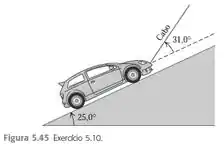
Um carro de está seguro por um cabo leve, sobre uma rampa muito lisa (sem atrito), como indicado na Figura . O cabo forma um ângulo de sobre a superfície da rampa, e a rampa ergue-se acima da horizontal.

a) Desenhe um diagrama do corpo livre para o carro.

b) Ache a tensão no cabo.

c) Com que intensidade a superfície da rampa empurra o carro?

(a) Sobre o carro estão agindo três forças:

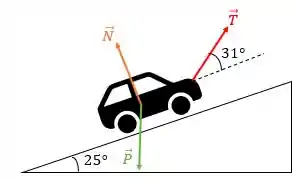
- A força peso vertical para baixo. Em relação ao eixo de coordenadas paralelo à rampa, a força peso está deslocada em por causa da inclinação da rampa;

- A força normal perpendicular à superfície de apoio (nesse caso, à rampa);

- A força de tração do cabo .

Fazendo o diagrama utilizando um eixo horizontal paralelo à rampa temos:

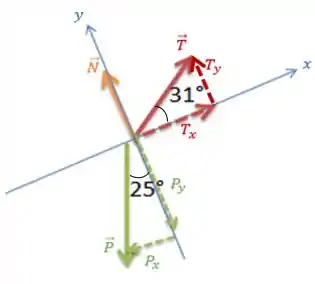
A força representada em laranja é a força normal , a força em verde é a força peso e os vetores verdes pontilhados representam suas componentes. E em vermelho está representado o vetor força de tensão no cabo . Também em pontilhado estão suas componentes.

(b) Todo sistema está em equilíbrio, então para determinar a tensão no cabo podemos aplicar a segunda lei de Newton ao longo do eixo horizontal:

Pela figura do DCL, conseguimos ver que e , então:

Isolando :

Como , no nosso carro temos :

Portanto,

(c) E a força que a superfície faz no carro é a força normal . Aplicando a segunda lei no eixo vertical teremos:

Pela figura do DCL, conseguimos ver que e , então:

Como já vimos o valor de e também podemos calcular :

Valeu, galera! Até a próxima! 😉