Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 28.Exercícios e Problemas - Ex. 46
Uma bola uniformemente carregada, de raio e com uma carga encontra-se no centro de uma casca metálica oca, com raio interno e raio externo . A esfera oca possui uma carga líquida .
a. Determine a intensidade de campo elétrico nas quatro regiões , , e .
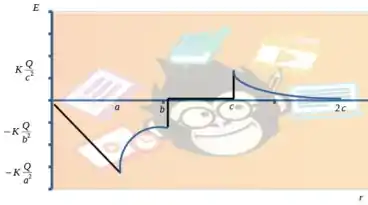
b. Desenhe o gráfico de E versus r desde até
Passo 1
Faaala aí galera
Primeiramente vamos escrever a equação do campo elétrico para
Vamos escrever a em termos da densidade de carga e volume
Nesta região, a carga é , esta região é delimitada pelo raio
Vamos substituir essa carga na Lei de Gauss
A área é
Vamos isolara o campo elétrico
E temos o campo elétrico
Passo 2
Para
Podemos utilizar a mesma equação
Vamos isolar o campo elétrico
Passo 3
Nesta região temos a esfera metálica, ou seja, um condutor. Então temos
O campo elétrico é nulo dentro de um condutor.
Passo 4
Aqui vamos usar a informação de que a carga liquida na esfera é
Somando com a carga negativa no interior da esfera, teremos
Passo 4
Vamos entender como vai ficar esse gráfico.
Vamos deixar em termos de uma constante
No passo 1 determinamos o valor até o raio , como nosso resultado foi um valor negativo, a função vai cair a uma taxa constante.
Já no passo 2, vai variar de acordo com ,ainda terminando num valor negativo
No passo 3 vimos que imediatamente ao entrar no condutor o Campo elétrico é zero e não varia com r.
E por fim, no passo 4 também temos uma função . A diferença é que dessa vez, ao aumentarmos a distância do campo elétrico ele vai tender a zero, pois já está fora da bola.
Resposta
a.
b.
(Passo 5)