Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 5.Problemas - Ex. 18

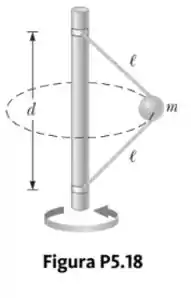
Por que a seguinte situação é impossível? O corpo de massa m   =   4,00   k g na Figura P5.18 é preso a uma haste vertical por dois barbantes de comprimento l   =   2,00   m . Os barbantes são presos à haste em pontos com d   =   3,00   m de distância entre eles. O corpo gira em um círculo horizontal com velocidade constante de v   =   3,00   m / s , e os barbantes permanecem esticados. A haste gira junto com o corpo de modo que os barbantes não se enrolam na haste.

E se? Esta situação seria possível em outro planeta?

Passo 1

E aiii gente, tudo bom com vocês?

Vamos fazer mais uma questão?

Bora comigo!

Abaixo, temos um diagrama para facilitar a compreensão:

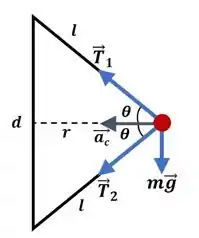
Calculando o ângulo:

sin ⁡ θ =   oposto     hipotenusa   = 1.5 2 θ = s i n - 1 ⁡ 1.5 2 = 48.6 ∘

Então, para r:

c o s ⁡ θ =   adjacente     hipotenusa = r 2

r = 2 c o s ⁡ 48.6 ∘ = 1.32 m

Uma vez que o objeto não acelera verticalmente, nós o modelamos como uma partícula em equilíbrio na direção vertical:

∑ F y = T 1 sin ⁡ 48.6 ∘ - T 2 sin ⁡ 48.6 ∘ - m g = 0 T 1 - T 2 sin ⁡ 48.6 ∘ = m g T 1 - T 2 = ( 4 ) ( 9.8 ) sin ⁡ 48.6 ∘ = 52.3 N

O objeto experimenta uma aceleração centrípeta na direção horizontal. Por isso é modelado como uma partícula em movimento circular uniforme nesta direção:

∑ F x = m a c = m v 2 r ∑ F x = T 1 c o s ⁡ 48.6 ∘ + T 2 c o s ⁡ 48.6 ∘ = ( 4 ) ( 3 ) 2 1.32

T 1 + T 2 cos ⁡ 48.6 ∘ = ( 4 ) ( 3 ) 2 1.32 T 1 + T 2 = ( 4 ) ( 3 ) 2 1.32 cos ⁡ 48.6 ∘ = 41.2 N

Passo 2

Somando as equações:

T 1 - T 2 + T 1 + T 2 = 52.3 + 41.2 = 93.5 2 T 1 = 93.5 T 1 = 93.5 2 = 46.9 N

T 2 = 41.2 - T 1 = 41.2 - 46.9 = - 5.7 N

As únicas variáveis ​​que podem ser alteradas são a velocidade do objeto (v) e a aceleração gravitacional (g). Da primeira equação:

T 1 - T 2 = ( 4 ) ( g ) sin ⁡ 48.6 ∘ = 5.33 g

T 1 - T 2 + T 1 + T 2 = 41.2 + 5.33 g 2 T 1 = 41.2 + 5.33 g

T 1 = 41.2 + 5.33 g 2 = 20.6 + 2.67 g

T 2 = 20.6 + 2.67 g - 5.33 g = 20.6 - 2.67 g

T 2 = 20.6 - 2.67 g > 0 2.67 g < 20.6 g < 7.72 m s 2

Conclusão: Esta situação pode ser possível em outro planeta com ( g <   7.72 m / s 2 .

Resposta

Ver resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Imagine que o quilograma-padrão seja colocado no equador terreste, onde se move em uma circunferência de raio 6,40 × 10 6m (raio da Terra) com uma velocidade escalar constante e 465m / s devido à rota
103- Uma corda pode suportar uma tração máxima de 40 N sem se partir. Uma criança amarra uma pedra de 0,37 kg em uma das extremidades da corda e, segurando a outra extremidade, faz a pedra girar em um
15. Um vagão de montanha-russa passa pelo topo de um loop vertical e circular com velocidade duas vezes maior do que a velocidade crítica. Qual é a razão entre a força normal e a força gravitacional?
16. A força normal iguala-se em intensidade à força gravitacional quando um vagão de montanha-russa passa pelo topo de um loop vertical com 40m de diâmetro. Quanto vale a velocidade do vagão no topo?
13. Um carro trafega sobre o topo de uma colina cujo raio é de 50m . Quanto vale a máxima velocidade que o carro pode ter sem que perca contato com a pista no topo da colina?