Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.Problemas Adicionais - Ex. 100

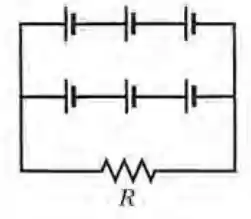
Cada uma das seis fontes reais da Fig. 27-68 possui uma força eletromotriz de 20 V e uma resistência de 4,0 Ω . (a) Qual é a corrente na resistência (externa) R = 4,0 Ω ? (b) Qual é diferença de potencial entre os terminais de uma das fontes? (c) Qual é a potência fornecida por uma das fontes? (d) Qual é a potência dissipada na resistência interna de uma das fontes?

Passo 1

Aqui temos seis fontes reais três em série e essas três em paralelo com outras três e uma resistência.

Passo 2

(a) Por simetria, sabemos que as correntes no ramo superior e no ramo central do circuito têm o mesmo valor, que vamos chamar de i. Isto significa que a corrente no resistor R do ramo inferior é i R = 2 i . Assim, chamando de r a resistência interna das fontes e de ε a fem das fontes e aplicando a regra das malhas à malha externa do circuito, obtemos

3 ε – i r – 2 i R = 0 ⇒ 3 ε = i 3 r + 2 R

logo

i = 3 ε 3 r + 2 R = 3 × 20 V 3 × 4 Ω + 2 × 4 Ω

resolvendo temos

i = 3,0 A

i R = 2 i = 6,0 A

Passo 3

(b)A diferença de potencial entre os terminais de uma das fontes é

Δ V = ε – i r = 20 V - 3,0 A × 4 Ω = 8,00 V

Passo 4

(c) De acordo com a Eq. 27-17, P f = i ε = 3 A × 20 V = 60 W .

Passo 5

(d) De acordo com a Eq. 26-27, P r = i 2 r = 3,0 A 2 × 4 Ω = 36 W .

Resposta

(a) i R = 6,0 A

(b) Δ V = 8,00 V

(c) P f = 60 W . (d P r = 36 W .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

De acordo com o teorema da superposição, a resposta (corrente) em um circuito é proporcional ao estímulo (voltagem) que a produz. Isso é verdade mesmo quando existem diversas fontes no circuito. Podem
27.37. Na Fig. 27-48 as resistências R 1 = 1,0Ω e R 2 = 2,0Ω e as forças eletromotrizes das fontes ideias são ξ 1 = 2,0V , ξ 2 = 4,0V e ξ 3 = 4,0V . Determine (a) o valor absoluto e (b) o sentido (par
a) Calcule a resistência equivalente (em termos de R, a resistência de cada um dos resistores) entre os pontos a e b para a escada infinita de resistores mostrada na Figura 25-80, considerando que os
Duas baterias com fems ε 1 e ε 2 e resistências internas r 1 e r 2 , estão conectadas em paralelo. Prove que, se um resistor de resistência R é conectado em paralelo ecom a combinação, a resistência ó
Na Figura 25-50, os valores das resistências estão relacionados como segue R 2 = R 3 = 2 R 1 . Se a potência P é fornecida a R 1 , qual é a potência fornecida a R 2 e a R 3 ?