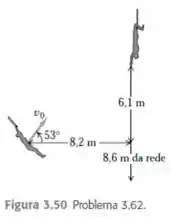
No trapézio voador. Em um novo circo, Maria oscila em um trapézio, projeta-se em um ângulo de e deve ser segurado por João, cujas mãos estão a acima e horizontalmente do ponto de lançamento de Maria (Figura ). Despreze a resistência do ar.

a) Qual deve ser a velocidade inicial de Maria para que ela seja segurada por João?

b) Para a velocidade inicial calculada em , qual é o módulo, a direção e o sentido da velocidade de Maria quando ela é segurada por João?

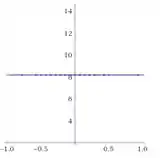
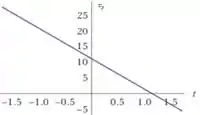
c) Supondo que Maria possua a velocidade inicial calculada em (a), faça diagramas , , e para o movimento dos dois trapezistas. Seus gráficos devem mostrar o movimento para cima até o instante em que Maria alcança João.

d) Na noite de estreia, João não consegue segurar Maria. Qual a distância horizontal percorrida por Maria, a partir de seu ponto inicial, até o momento em que ela atinge a rede de segurança situada a abaixo de seu ponto inicial?

Agora é só substituir os valores que temos e lembrar que a aceleração da gravidade vale . Daí ficamos só com a variável :

Jogando tudo isso na calculadora chegamos ao valor da velocidade inicial,

Show?

Para achar o módulo e a direção precisamos das componentes verticais horizontais do vetor velocidade. Na horizontal temos:

E na vertical o movimento não é constante, então precisamos determinar o instante que a Maria é segurada pelo João. Na posição e com velocidade o tempo é:

E da equação pra velocidade no MRUV:

E o módulo da velocidade vai ser:

E a direção é dada pela tangente do ângulo inicial:

Bacana, não é?

Agora vamos aos gráficos!

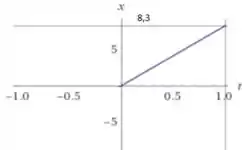
Maria parte da origem e em ela encontra o João na posição . Na horizontal o movimento dela é constante, com velocidade . Na vertical o movimento dela é variado, com velocidade inicial de . As equações de movimento e seus respectivos gráficos são:

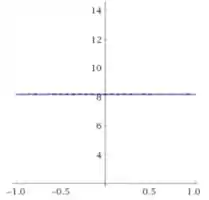
• Na horizontal:





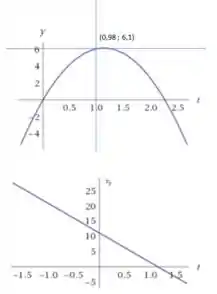
• Na vertical:

Tranquilo até aqui?

Usando a equação que já usei lá no passo :

Usando os mesmos valores iniciais de temos:

E o problema pede a distância horizontal quando :

Ficamos com uma equação de segundo grau em . Usando bhaskara teremos as raízes:

Jogando tudo isso na calculadora e pegando a solução positiva:

E aí! o que achou? Responde Aí!