Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 63

Um carro parte do repouso em uma curva com raio de 120   m e acelera a 1,0   m / s . Que ângulo terá descrito o carro quando o módulo de sua aceleração total for 2,0   m / s 2 ?

Passo 1

  1. Vamos usar o Movimento Circular Não Uniforme, a aceleração é

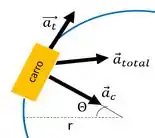
Os dados que o exercício fornece

a t = 1,0   m / s 2

r = 120   m

a t o t a l = 2,0   m / s 2

E tem que encontrar θ .

Passo 2

a. Na equação seguinte, vemos que a velocidade é numericamente igual ao tempo

v = v 0 + a y t - t 0 → v = 0 + 1 t - 0 → v = t

Usando v = t , vamos substituir t na equação da aceleração tangencial, dessa forma

a t = v 2 r = t 2 120   m / s 4

O exercício nos forneceu que a aceleração total é de 2   m / s 2 , como se trata de uma equação vetorial, faremos

a t o t a l → = a t → + a c →

2 = a t 2 + a c 2 → 2 = 1 + t 2 120 2 → 2 2 = 1 + t 2 120 2 2 →

4 = 1 + t 2 120 2 → 3 = t 4 14400 → 3 × 14400 = t 4 → t = 14,4   s

Agora para descobrir θ faremos

θ = θ 0 + ω t - t 0 + a t - t 0 2 2 r → θ = 0 + 0 + 1 × 14,4 2 2 × 240 → θ = 0,864   r a d

Resposta

θ = 0,864   r a d

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um velocista corredo em uma pista circular possui uma velocidade escalar constante de 9,2m / s e uma aceleração centrípeta de módulo 3,8m/s² ². Quais são (a) o raio da pista e (b) o período do movimen
Você pretende atirar uma bola com uma velocidade escalar de 12,0m / s em um alvo que está a uma altura h = 5,00m acima do núvel do qual você vai lançar a vola (veja a figura). Você quer que a velocida
105- Existem relatos de guepardos correndo à velocidade impressionante de 114 km/h, feitos por observadores que dirigiam ao lado desses animais. Imagine o que é tentar medir a velocidade de um guepard
Astronautas usam uma centrífuga para simular a aceleração de um foguete durante um lançamento. A centrífuga leva 30s para acelerar desde o repouso até sua velocidade de rotação máxima, que é 1 rotação
Uma típica centrífuga de laboratório gira a 4.000 rpm. Tubos de ensaio são colocados na centrífuga com muito cuidado por causa das grandes acelerações desenvolvidas.a. Qual é a aceleração na extremida