Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 4.Problemas - Ex. 59
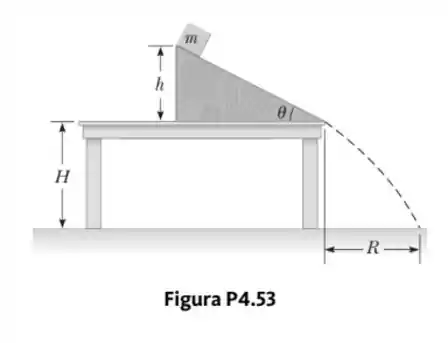
Na Figura P4.53, o plano inclinado tem massa e é fixado ao tampo da mesa horizontal fixa. O bloco de massa é colocado próximo à base do plano inclinado e é solto com um impulso rápido que o faz deslizar para cima. O bloco para perto do topo do plano inclinado, como mostrado na figura e, em seguida, desce novamente, sempre sem atrito. Encontre a força que a mesa exerce sobre o plano inclinado durante todo esse movimento em termos de , , e .
Passo 1
E aiii galera, vamos fazer uma questão aqui?
Vem comigo!
Vamos primeiro desenhar para facilitar:
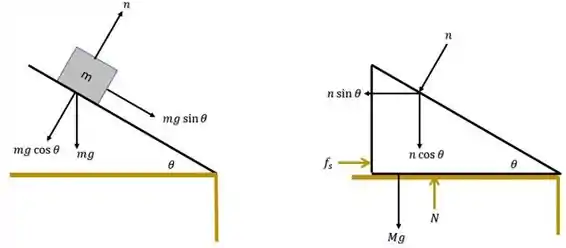
Passo 2
Aplicando segunda Lei de Newton:
E agora, na direção vertical:
Aplicando a segunda lei de Newton à inclinação na direção horizontal, temos:
Então, a força total é:
Resposta
Exercícios de Livros Relacionados
Um bloco começa a subir um plano inclinado sem atrito com uma velocidade inicial v 0 = 3,50m / s . O ângulo do plano inclinado é θ = 32,0 ° . (a) Que distância ao longo do plano inclinado o bloco cons
Na Fig. 5-40, um caixote de massa m = 100k g é empurrado por uma força horizontal F → que o faz subir uma rampa sem atrito ( θ = 30,0 ° ) com velocidade constante. Quais são os módulos (a) de F → e (b
Um plano sem atrito tem 10,0m de comprimento e 35,0 ° de inclinação. Um trenó começa na parte de baixo com velocidade inicial de 5,00m / s subindo o declive. Quando ele alcança o ponto no qual momenta
Uma cunha de massa M repousa sobre o topo horizontal de uma mesa sem atrito. Um bloco de massa m é colocado sobre a cunha (Figura P5.112a). Não existe nenhum atrito entre o bloco e cunha. O sistema é
Uma cunha de massa M repousa sobre o topo horizontal de uma mesa sem atrito. Um bloco de massa m é colocado sobre a cunha e uma força horizontal F é aplicada sobre ela (Figura P5.112b). Qual deve ser