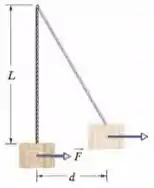
Um caixote de está pendurado na extremidade de uma corda de comprimento . Você empurra o caixote horizontalmente com uma força variável , deslocando-o para o lado de uma distância (Fig. 7-43). (a) Qual é o módulo de quando o caixote está na posição final? Neste deslocamento, quais são (b) o trabalho total realizado sobre o caixote, (c) o trabalho realizado pela força gravitacional sobre o caixote e (d) o trabalho realizado pela corda sobre o caixote? (e) Sabendo que o caixote está em repouso antes e depois do deslocamento, use as respostas dos itens (b),(c) e (d) para determinar o trabalho que a força realiza sobre o caixote. (f) Por que o trabalho da força não é igual ao produto do deslocamento horizontal pela resposta do item (a)?
Passo 1
Vamos iniciar esta questão fazendo o DCL do caixote:
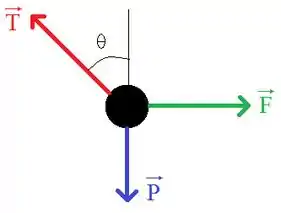
Como o enunciado nos diz que o caixote está em repouso nesta situação, então, aplicando a segunda lei de Newton aos eixos (horizontal) e (vertical):
E para determinar o ângulo precisamos usar a relação trigonométrica no triângulo retângulo:
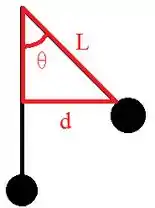
A partir da ilustração acima, sabemos que:
Então, isolando :
Passo 2
Com o ângulo já calculado, precisamos determinar para, então, determinar o valor de . Para isso, usaremos inicialmente a :
Passo 3
Com o valor de em mãos, podemos usar a para determinar :
Passo 4
O trabalho entre o ponto inicial e o ponto final é nulo, pois, aplicando o teorema trabalho-energia cinética, temos:
Como inicialmente ele estava em repouso e na posição final ele também está em repouso, a variação da energia cinética é nula e, portanto, o trabalho total também é nulo:
Passo 5
O trabalho realizado pela força peso pode ser calculado a partir da seguinte relação:
Assim:
Passo 6
Como a força da corda está sempre perpendicular ao movimento, então o trabalho realizado por ela é nulo.
Passo 7
Para determinar o trabalho realizado pela força vamos usar o teorema trabalho-energia cinética:
Como o caixote está em repouso na posição inicial e final, então:
Substituindo os valores calculados e isolando :
Passo 8
Porque se observarmos a percebemos que a força varia com o tempo, entretanto, só podemos usar a equação de força vezes o deslocamento para forças constantes.
Resposta
- ;
- ;
- ;
- ;
- ;
- .