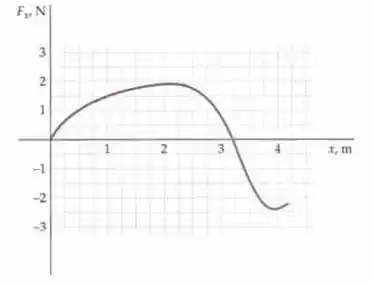
Um corpo de 3,0 kg, que se move ao longo do eixo x, tem urna velocidade de +2,4 m/s quando passa pela origem. Ele está sujeito a uma força única, , que varia com a posição como mostrado na figura abaixo. a) Encontre o trabalho realizado pela força de x = 0.0 m até x = 2,0 m. (b) Qual é a energia cinética do corpo em x = 2,0 m? (c) Qual é a rapidez do objeto em x = 2,0 m? (d) Qual é o trabalho realizado sobre o corpo de x = 0,0 m até x = 4,0 m? (e) Qual é a rapidez do corpo em x = 4,0 m?
Passo 1
Letra (a)
Falaa!
Ele quer o trabalho realizado por sobre a partícula e a gente tem o gráfico que relaciona como o deslocamento da partícula.
Lembra que o trabalho é dado pela área abaixo da curva do gráfico força versus deslocamento!
Como a força e o deslocamento são paralelos, no nosso caso, o trabalho realizado por é dado pela área do nosso gráfico entre e .
Vamos calcular a área abaixo do gráfico contando quadradinhos. Tem mais ou menos 22 quadradinhos. A altura de um quadradinho e a largura é . Então o trabalho equivalente a um quadradinho é
Se temos 22 quadradinhos abaixo da curva até , então o trabalho nesse intervalo vai ser
Passo 2
Letra (b)
Queremos a energia cinética em . Cara, falou de trabalho e rapidez no mesmo contexto, cê pensa logo no teorema do trabalho-energia cinética. Olha a expressão dele:
Isso diz que o trabalho total feito em uma partícula é igual à variação de energia cinética.
E lembra que temos o trabalho total realizado sobre a partícula na direção até (o trabalho realizado por que calculamos no item a)
E podemos calcular a energia cinética inicial em porque ele deu a velocidade nesse ponto e a massa . Usando a expressão da energia cinética:
Substituindo essas coisas no teorema, conseguimos achar a energia cinética final, que para esse caso, é a energia cinética em .
Passo 3
Letra (c)
Pela energia achada no item (b), tiramos a rapidez do objeto. Como? Usando a expressão da energia cinética em :
Isolando o :
Substituindo os valores, lembrando que é a energia cinética em que calculamos no passo anterior:
Passo 4
Letra (d)
Novamente vamos calcular a área abaixo do gráfico de até para achar o trabalho realizado. Mas repara que temos uma área cima do eixo horizontal e abaixo dele.
A área abaixo dele vai entrar negativa na nossa continha porque ali a força mudou de sentido (já que fica negativa). Então vamos contar quantos quadrados temos acima do eixo horizontal e abaixo:
- acima: 35, entram positivos
- abaixo: 9, entram negativos
Um quadrado vale . Assim o trabalho entre e fica:
Passo 5
Letra (e)
Vimos que pelo teorema trabalho-energia:
O ponto inicial é a origem e o final é , de onde queremos a rapidez.
Substituindo a expressão da energia cinética para cada termo:
Queremos , então vamos isolar essa bonita:
Subsituindo os dados e lembrando que calculamos no item anterior:
Resposta
Letra (a):
Letra (b):
Letra (c):
Letra (d):
Letra (e):