Quando calculamos uma rapidez de escape, usualmente o fazemos na suposição de que o corpo lançado está isolado. Isto é, obviamente, geralmente incorreto no sistema solar. Mostre que a rapidez de escape em um ponto próximo de um sistema consistindo de dois corpos massivos, estacionários e esféricos, é igual à raiz quadrada da soma dos quadrados dos valores de rapidez de escape para cada um dos corpos considerados individualmente.
Passo 1
Vamos lá, uma coisa por vez. O sistema que o problema descreve tem dois corpos massivos de massas e , respectivamente, e um corpo de massa localizado no ponto que estamos analisando nesse sistema. O sistema é o seguinte:
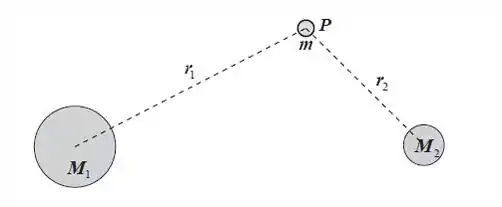
A questão quer que provemos que a velocidade de escape total será dada por:
Lembre-se que a velocidade de escape em um sistema com um corpo massivo é:
Passo 2
Vamos usar as expressões de energia cinética e potencial para resolver o nosso problema. Ficamos então com o seguinte para a energia total do sistema:
Passo 3
Quando o objeto escapa de ambas as órbitas, sua energia total será zero e ele terá a velocidade de escape. Colocando isso na nossa equação acima:
E repare que cada um desses termos no lado direito da equação é o quadrado da velocida de escape que definimos lá em cima! Então vamos ficar com:
Ou seja:
Que é exatamente o que queríamos provar!
Resposta
Ei, a resposta está no passo a passo :)