Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 11.1 - Ex. 55

Calcule a mínima rapidez necessária, em relação à Terra, para que um corpo lançado da superfície da Terra escape do sistema solar. A resposta dependerá da direção do lançamento. Explique a escolha de direção de lançamento que você faria com o objetivo de minimizar a necessária rapidez de lançamento em relação à Terra. Despreze o movimento rotacional da Terra e a resistência do ar.

Passo 1

Antes de tudo, vamos amos colocar esse problema numa imagem pra facilitar a visualização das coisas:

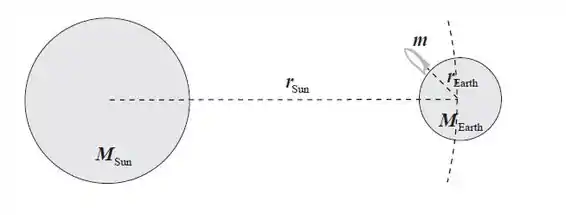
Essa é a posição inicial do Sol, da Terra e do foguete.

Passo 2

No problema anterior nós mostramos que a velocidade de escape num sistema de dois corpos massivos é dada por:

v e 2 = 2 G M 1 r 1 + 2 G M 2 r 2

Vamos resolver essa equação e teremos v e .

v e = 2 G M T e r r a r T e r r a + M S o l r S o l

Agora substituindo os valores:

v e = 2 6.67 ∙ 10 - 11   m 3 k g - 1 s - 2 5.97 ∙ 10 24   k g 6.37 ∙ 10 6   m + 1.99 ∙ 10 30   k g 1.496 ∙ 10 11   m = 43.6   k m / s

O valor que acabamos de encontrar é a velocidade de escape da Terra na órbita da Terra, mas nós queremos a velocidade mínima! Essa velocidade mínima acontece quando nos aproveitamos da velocidade da órbita da Terra. Então considerando a velocidade da órbita da Terra, vamos ficar com:

v m í n = v e - v ó r b i t a

Passo 3

Agora só precisamos encontrar essa velocidade da órbita! Isso não é problema para nós. Vamos ficar com o seguinte:

v ó r b i t a = 2 π   r ó r b i t a T ó r b i t a

Esse T ó r b i t a é o tempo para uma volta completa da Terra ao redor do Sol, ou seja, 365.24 dias. Isso em segundos será:

T ó r b i t a = 365.24   d ∙ 24   h ∙ 60   m ∙ 60   s = 31.57 ∙ 10 6   s

Passo 4

Agora substituindo v ó r b i t a na fórmula do v m í n :

v m í n = v e - 2 π   r ó r b i t a T ó r b i t a

E agora é só substituir os valores!

v m í n = 43.6 k m s - 2 π 1.496 ∙ 10 11   m 31.57 ∙ 10 6   s = 13.8   k m / s

Resposta

v m í n = 13.8   k m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que a aceleração da gravidade na Lua é 0 , 166 vezes aquela na Terra, e que o raio da Lua é 0,273R T , determine a rapidez de escape de um projétil lançado na superfície da Lua.
(a) Se tomamos como zero a energia potencial de um corpo de 100k g e a Terra, quando os dois corpos estão separadas de uma distancia infinita, qual é a energia potencial quando corpo está na superfíci
Preparando seu orçamento para o próximo ano, a NASA deseja relatar para a nação uma aproximada do custo (por quilograma) de se lancar um satélite moderno em uma orbita próxima da Terra. Voce é escolhi
Qual é a rapidez inical necessária para que uma partícula lançada da superfície da Terra tenha uma rapidez final igual à sua rapidez de escape quando estiver muito distante da terra? Despreze a resist
A força exercida pela terra sobre uma particula de massa m a uma distancia r( rR T ) do centro da Terra tem por magnitude m g R T 2 / r 2 , onde g = G M T / R T 2 . (a) Calcule o trabalho que você dev