Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 18.Exercícios e Problemas - Ex. 11
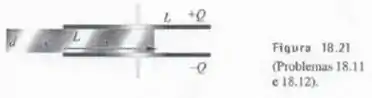
Calcule a capacitância do capacitor mostrado na Figura 18.21.
Passo 1
Nós podemos olhar para esse problema como dois capacitores de placas paralelas associado em paralelo: um com comprimento preenchido pelo dielétrico e outro com comprimento preenchido por vácuo.
Para um capacitor de placas paralelas de área , distância entre as placas no vácuo, temos que
Nesse caso, o capacitor 1 (preenchido pelo dielétrico) tem capacitância:
Já o capacitor 2 tem capacitância
Como os capacitores estão em paralelo, a capacitância equivalente do sistema será
Passo 2
Vamos supor que a área do total da placa é , de modo que
Seja a largura da placa, de modo que
Com isso achamos
Portanto,
Ou ainda,
Observe que para nós retomamos o resultado esperado para o vácuo!
Resposta
Exercícios de Livros Relacionados
A Figura 18.18 mostra uma esfera metálica de raio igual a 1,00c m , com carga de 0,100μ C , incrustada em uma esfera concêntrica de náilon, cujo raio é 3,00c m . Calcule a densidade superficial de car
Calcule o valor da polarização elétrica à distância r = 10c m do centro de uma pequena esfera metálica possuindo carga de 1,00 ⋅ 10 - 12C , imersa em um meio homogêneo de constante dielétrica κ = 2,00
As faces de uma folha de mica, de espessura igual a 30μ m , são metalizadas para formar um capacitor, como mostra a Figura 18.16.a) Por que uma estreita faixa próxima às bordas é deixada sem metalizaç
O campo elétrico no interior de um meia cuja suscetibilidade elétrica varia na forma χ = a x , onde a é uma constante, é constante, com valor E → = Ei → . Calcule:a) A expressão para a polarização elé
Esboce as linhas de força do campo elétrico referentes à figura 18.18, utilizando as informações dados no Problema 18.6.