Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 18.Exercícios e Problemas - Ex. 15
Calcule a capacitância do capacitor mostrado na figura 18.23.
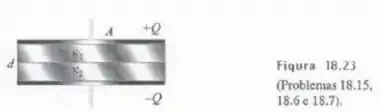
Passo 1
Podemos olhar para esse problema como se fossem dois capacitores em série, um com capacitância e outro com capacitância :
Para o primeiro capacitor, temos
Já para o segundo,
Com isso,
Passo 2
Mas observe que
Creio que faltou essa informação no enunciado, mas vou supor que seja isso mesmo que está de bom acordo com a figura! Portanto,
Invertendo a relação, achamos a capacitância do sistema:
Resposta
Exercícios de Livros Relacionados
Uma linha infinita de carga produz um campo de 4,52 × 10 4 N / C a uma distância de 1,96m . Calcule a densidade de carga linear.
Um capacitor de placas paralelas cheio de ar tem uma capacitância de 50 pF. (a) Sabendo-se que suas placas têm uma área de 0,35m 2 qual é a separação entre elas? (b) Se a região entre as placas for pr
Um cabo coaxial usado numa linha de transmissão tem um raio interno de 0 , 10m m e um raio externo de 0,60m m . Calcular a capacitância por metro de cabo. Suponha que o espaço entre os condutores seja
Deseja-se construir um capacitor cuja capacitância se aproxime de 1 nF e um potencial de ruptura acima de 10.000 V. Com esse objetivo, podemos usar os lados de um copo grande de pírex cobrindo as part
Um capacitor de placas paralelas cheio de ar tem uma capacitância de 1,3 pF. Dobra-se a separação das placas e insere-se parafina entre elas. A nova capacitância é 2,6 pF. Determine a constante dielét