Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 18.Exercícios e Problemas - Ex. 13
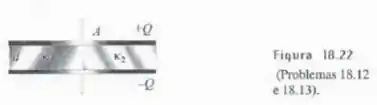
Calcule a capacitância do capacitor mostrado na figura 18.22.
Passo 1
Podemos olhar para esse problema como se fossem dois capacitores em paralelo, um com capacitância e outro com capacitância :
Para o primeiro capacitor, temos
Já para o segundo,
Somando os dois
Passo 2
Mas note que cada dielétrico ocupa metade da área do capacitor, de modo que
Assim
Essa é a capacitância do sistema!
Resposta
Exercícios de Livros Relacionados
Calcule:a) a força F x exercida sobre o bloco dielétrico da Figura 18.21, sabendo-se que suas grandes faces e as placas do capacitor são quadrados de lado L ;b) Calcule o valor numérico de F para x =
Calcule a capacitância do capacitor mostrado na figura 18.23.
A constante dielétrica do capacitor visto na Figura 18.24 varia linearmente com a coordenada y , na forma κ = 1 + κ d - 1 y / d . Calcule os campos D y , E y e P y dentro do dielétrico.
Determine a capacitância do capacitor de placas paralelas mostrado na figura 24-44.