Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 18.Exercícios e Problemas - Ex. 12
Calcule:
a) a força exercida sobre o bloco dielétrico da Figura 18.21, sabendo-se que suas grandes faces e as placas do capacitor são quadrados de lado ;
b) Calcule o valor numérico de para , , , e .
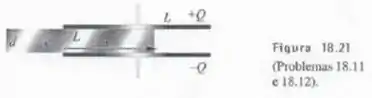
Passo 1
No exercício anterior nós achamos a expressão para a capacitância do sistema em função de :
Como , temos que
Como a carga entre os capacitores é constante, vamos usar a seguinte expressão para a energia potencial do sistema
A força será dada por
Ou ainda,
Passo 2
Derivando a expressão da capacitância:
Assim,
Substituindo a expressão da capacitância:
Portanto,
Ou ainda,
Passo 3
Substituindo os valores:
Portanto,
Resposta
Exercícios de Livros Relacionados
O espaço entre as placas de um capacitor que está conectado aos terminais de uma bateria é preenchido com um material dielétrico. Determine a constante dielétrica do material se a carga ligada induzid
A placa carregada positivamente de um capacitor de placas paralelas tem carga igual a Q . Quando é feito vácuo no espaçamento entre as placas, a intensidade do campo elétrico entre elas é 2,2. 10 5V /
Calcule:a) a polarização elétrica em cada um dos dielétricos do capacitor visto na Figura 18.23;b) a densidade superficial de carga de polarização na interface entre os dois dielétricos.
Com referência ao capacitor visto na Figura 18.22, calcule:a) o deslocamento elétrico nos dois dielétricos;b) a polarização dos dois dielétricos;c) as cargas elétricas nas metades 1 e 2 das placas.
Um capacitor é feito com uma folha de PVDF (constante dielétrica 11 e rigidez dielétrica 1,0 ⋅ 10 2k V / m m ). A folha tem espessura de 5,0μ m , e em uma de duas faces é depositado um filme de alumín