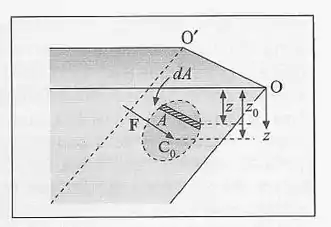
4. Calcule a magnitude da força exercida por um fluido sobre uma área de parede plana( inclinada de um ângulo qualquer em relação à vertical), do recipiente que o contém. Para isto, divida a área em faixas infinitesimais horizontais (uma delas é mostrada hachurada na Fig. P.4); seja a profundidade de , e a densidade do fluido. (a) Mostre que , onde é a profundidade do centróide de , definido como a profundidade do centro de massa de , considerado como uma placa plana homogênea. (b) O torque resultante sobre , em relação a um eixo horizontal , é o mesmo que se a força estivesse aplicada num ponto da área (veja Fig. P.4), que se chama centro das pressões. Motre que a profundidade do centro das pressões é dada por , onde é análogo a um “momento de inércia” de em relação a .

Em seguida, o que temos que fazer é lembrar que a coordenada central centróide de uma placa homogênea pode ser obtido a partir de:

Rearrajando essa expressão, alcançamos que:

Ótimo! Maravilha! Tudo que temos de fazer para resolver essa letra em definitivo, é substituir esse último resultado naquela última relação do :

b) Nessa letra, o que queremos é encontrar o torque aplicado em cad a uma das tiras infinitesimais. Esse torque é o produto entre a força aplicada sob a tira e a distância em relação ao eixo , isto é, :

Só que , lá do , sabemos ser dado por:

O que nos faz ficar com:

Seguindo nosso caminho, bora integrar essa epxressão pra ver o que dá:

Que beleza! Sabe o porquê? Lá do enunciado, obtemos que . O que nos dá:

Agora sim, já sabemos que esse torque é equivalente ao torque resultante devido àforça aplicada no centro das pressões , que está à uma distância vertical da origem. Deste modo, e o torque, em termos de é:

Igualemos então, essa expressão e a do final do :

Pronto! Encontramos a resposta que queríamos!