Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 1.Problemas - Ex. 1

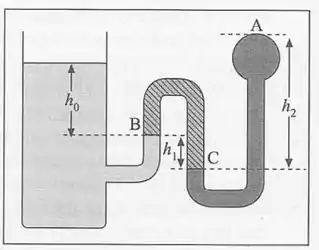
1. No sistema da Fig . P . 1 , a porção A C contém mercúrio, B C contém óleo e o tanque aberto contém água. As alturas indicadas são: h 0 = 10   c m , h 1 = 5   c m , h 2 = 20   c m e as densidades relativas são: 13,6   (mercúrio) e 0,8 (óleo). Determine a pressão p A no ponto A ( em a t m ) .

Passo 1

Bora lá pro nosso primeiro probleminha nesse maravilhoso e complicado livro de Física.

Ao olhar a nossa figurinha do enunciado, a primeira coisa que temos de fazer é definir algumas coisas. Por isso, bora separa a nossa figura em trechos. O primeiro trecho vai da superfície da água até o ponto B . E nesse ponto, a pressão devido a coluna de água é:

P B = P 0 + ρ 0 g h 0

Onde ρ 0   representa a densidade da água e P 0   a pressão atmosférica.

Passo 2

Já para o nosso trecho B C , a pressão no ponto C é devido a pressão que a coluna de água exerce na linha na altura do ponto B somada com a pressão devido à coluna de óleo de altura   h 1   . Desse modo, a pressão em C vale:

P C = P B + ρ 1 g h 1

Só que do P a s s o   1 :

P B = P 0 + ρ 0 g h 0

O que nos leva à seguinte relação:

P C = P 0 + ρ 0 g h 0 + ρ 1 g h 1

Passo 3

Por fim!! Tomemos agora o trecho que vai de A até C . O ponto A , por estar numa altura acima de C , vai ter uma pressão menor que a pressão em C . Sabemos então, que a contribuição devido à pressão no ponto A e a coluna de mercúrio de altura h 2   na altura da linha que passa pelo ponto C deve ser igual à P C   ... Deste modo:

P C = P A + ρ 2 g h 2

Só que do P a s s o   2 :

P C = P 0 + ρ 0 g h 0 + ρ 1 g h 1

O que nos fornece a seguinte identidade:

P A + ρ 2 g h 2 = P 0 + ρ 0 g h 0 + ρ 1 g h 1

P A = P 0 + ρ 0 g h 0 + ρ 1 g h 1 - ρ 2 g h 2

Onde temos os seguintes valores:

P 0 = 1   a t m ≈ 1,01 ⋅ 10 5   P a ρ 0 = 1   g / c m 3 = 1000   k g / m 3 ρ 1 = 0,8   g / c m 3 = 8 00   k g / m 3 ρ 2 = 13,6   g / c m 3 = 13600   k g / m 3

Basta então substituir esses valores na fórmula, juntamente com as alturas, que precisam estar em metros:

P A = P 0 + ρ 0 g h 0 + ρ 1 g h 1 - ρ 2 g h 2

P A = [ 1,01 ⋅ 10 5   + 1000 ⋅ 9,81 ⋅ 0,1 + 800 ⋅ 9,81 ⋅ 0,05 - 13600 ⋅ 9,81 ⋅ 0,2 ]   P a

P A = 75690   P a = 75690 10100   a t m ≈ 0,75   a t m

Pronto! Resposta encontrada!

Resposta

P A = 75690   P a = 75690 101000   a t m ≈ 0,75   a t m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Verifique o resultado da experiência do Puy de Dome, realizada por Périer em 1648.
Um carro de 975 kg tem os seus pneus cheios a ’32,0 libras’. (a) Quais são a pressão absoluta e a pressão manométrica nesses pneus em l i b r a s / p o l e g a d a s 2 , P a e a t m ? (b) Se os pneus
14.22a. O tanque em forma de L mostrado na Fig. 14-36 está cheio d’água e é aberto na parte de cima. Se d=5,0m , qual é a força exercida pela água na face A?
23. Um grande aquário de 5,00m de altura está cheio de água doce até uma altura de 2,00m . Uma das paredes do aquário é feita de plástico e tem 8,00m de largura. De quanto aumenta a força exercida sob
Dois recipientes cilíndricos iguais, com as bases no mesmo nível, contêm um líquido de massa específica 1,30 × 10 ³k g / m ³ . ³ ³ A área de cada base é 4,00c m ² ², mas em um dos recipientes a altura