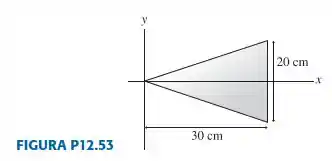
|| Calcule o momento de inércia da chapa de aço da para rotações em torno de um eixo perpendicular à chapa e que passa pela origem.
Passo 1
A chapa é um triângulo com :
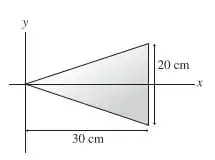
Nós podemos aplicar uma fórmula direta do momento de inercia.
Passo 2
Vamos trabalhar no que é a massa, ele pode se relacionar com a área .
Podemos fazer:
é uma mostra muito pequena de área que pode ser expresso por .
é uma amostra muito pequena da massa total.
é a massa de
é a área total da chapa, que é um triangulo e vale
Então:
Passo 3
Agora temos
Como temos e , vamos transformar em integral dupla com os intervalos de e O intervalo de é , se nós olharmos para as arestas do triangulo.
Fica: