Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 58
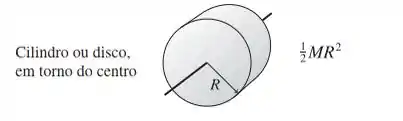
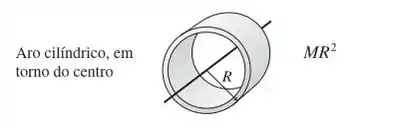
58. || Um disco de massa e raio tem um buraco de raio r centrado no eixo de simetria. Calcule o momento de inércia do disco.
Confirme se sua resposta concorda com a quando e quando .
c. Um disco de de diâmetro com um buraco de de diâmetro desce rolando uma rampa com de comprimento e de inclinação. Qual é o valor da velocidade na base da rampa? Isso corresponde a que percentagem da rapidez de uma partícula que desliza por esta rampa sem atrito?
Passo 1
Um disco de massa e raio tem um buraco de raio centrado no eixo de simetria. Calcule o momento de inércia do disco.
Por conta da ausência de dados, precisaremos usar derivadas e integrais e achar o que a questão pede. Mas não se preocupe, é fácil. Vamos deduzir algumas coisas e partir par letra a.
Um esquema para o disco é:
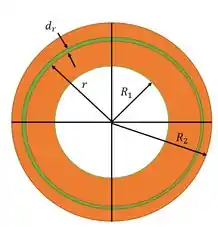
Em verde uma amostrazinha, ela necessária para poder usar derivada mas a frente.
Passo 2
Podemos determinar a área do disco:
Podemos usar a ideia de derivada agora. Uma pequena parte de massa sobre o todo de massa. E também uma outra pequena parte de área sobre um todo de área:
Mas nós já temos , então:
Passo 3
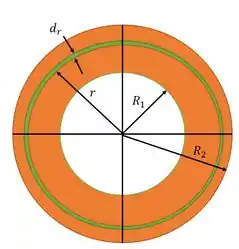
Veja que o pode se relacionar com o e, pelo comprimento de uma circunferência:
Então podemos reescrever o :
E agora achamos o momento de inercia pela definição dele:
Passo 4
Confirme se sua resposta concorda com a quando e quando .
Se :
Pela este é o momento de inércia para um disco ou cilindro sólido sobre o centro.
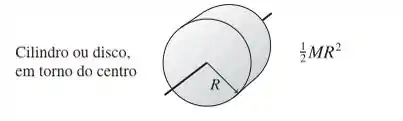
Se
Pela esta é a expressão para o momento de inércia de um aro cilíndrico ou toque no centro.
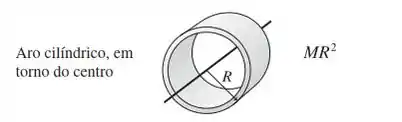
Passo 5
c. Um disco de de diâmetro com um buraco de de diâmetro desce rolando uma rampa com de comprimento e de inclinação. Qual é o valor da velocidade na base da rampa? Isso corresponde a que percentagem da rapidez de uma partícula que desliza por esta rampa sem atrito?
Um esquema para a letra seria:
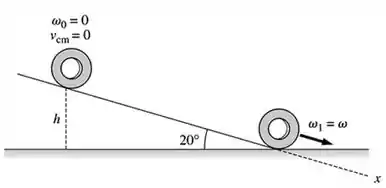
A rampa mede . Então o vai ser :
A energia potencial gravitacional inicial do disco é transformada em energia cinética à medida que rola para baixo. Podemos aplicar a lei de conservação de energia mecânica. Fica:
Já temos e , desenvolvendo:
Substituindo os dados com e
Isso corresponde a que percentagem da rapidez de uma partícula que desliza por esta rampa sem atrito?
Usando conservação de energia, para velocidade final e inicial de uma partícula:
A razão será:
Resposta
