Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 2

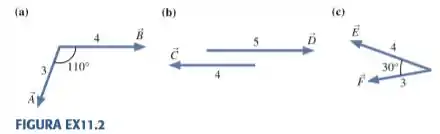
Calcule o produto escalar dos três pares de vetores da FIGURA EX11.2

Passo 1

O produto escalar de um par de vetores u e v é definido pela seguinte expressão:

< u ,   v > = u ∙ v ∙ cos ⁡ θ

Onde < u ,   v > é a representação do produto escalar, u e v são os módulos dos vetores u e v , respectivamente, e θ é o ângulo (inferior a π = 180 ° ) formado entre os vetores.

O produto escalar entre vetores, então, como você vai ver, resulta em um número (um escalar), e não em um vetor!

Com a definição, conseguimos calcular facilmente os produtos escalares da figura.

Passo 2

  1. Temos como módulos dos vetores os valores u = 3 e v = 4 (a ordem aqui não importa)!, e como ângulo θ = 11 0 ° . Aplicamos na definição e vamos ter:

    2. < u ,   v > = 3 ∙ 4 ∙ cos ⁡ 11 0 ° =

    ≅ - 4 , 10

    Passo 3

  2. Temos como módulos dos vetores os valores u = 4 e v = 5 (a ordem aqui não importa)!, e como ângulo θ = 1 8 0 ° , já que os vetores estão paralelos. Aplicamos na definição e vamos ter:

    3. < u ,   v > = 4 ∙ 5 ∙ cos ⁡ 1 8 0 ° =

    = - 20

    Passo 4

  3. Temos como módulos dos vetores os valores u = 3 e v = 4 (a ordem aqui não importa)!, e como ângulo θ = 30 ° . Aplicamos na definição e vamos ter:

< u ,   v > = 3 ∙ 4 ∙ cos ⁡ 3 0 ° =

≅ 10,4

E, aqui, você pode perceber que o produto escalar entre vetores com um ângulo agudo ( θ < 90 ° ) vai ser positivo; entre vetores com um ângulo obtuso ( θ > 90 ° ) será negativo; entre vetores com um ângulo reto ( θ = 90 ° ) será nulo.

Resposta

  1. -4,10

  2. -20

  3. 10,4
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

64 . A constante elástica de uma suspensão de automóvel cresce com o aumento de carga por causa de uma mola que é mais larga na parte inferior, estreitando-se suavemente a um diâmetro menor perto da p
Uma criança com 20 kg de massa desliza sem atrito em um tobogã, descendo uma altura de 3,0 m. Calcule:A) O trabalho realizado pelo tobogã sobre a criança.B) O trabalho realizado pela gravidade sobre a
Um pacote de 12,0k g em uma sala de distribuição de encomendas desliza por 2,00m rampa abaixo, inclinada em 53,0 ° abaixo do plano horizontal. O coeficiente de atrito cinético entre o pacote e a super
Um engradado grande encontra-se sobre o piso de um depósito. Paulo e Beto aplicam forças horizontais constantes sobre o engradado. A força aplicada por Paulo tem módulo 48,0N no sentido 61,0 ° do oest
Você aplica uma força constante F → = - 68,0N i ^ + 36,0N j ^ a um carro de 380k g enquanto o carro percorre 48,0m a 240,0 ° em sentido anti-horário a partir do eixo x positivo. Qual é o trabalho real