Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 6.1 - Ex. 10
Um pacote de em uma sala de distribuição de encomendas desliza por rampa abaixo, inclinada em abaixo do plano horizontal. O coeficiente de atrito cinético entre o pacote e a superfície da rampa é . Calcule o trabalho realizado sobre o pacote por (a) atrito, (b) gravidade e (c) a força normal. (d) Qual é o trabalho resultante realizado sobre o pacote?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar o trabalho realizado sobre o pacote por atrito, pela gravidade e pela força normal e determinar o trabalho resultante realizado sobre o pacote.
O primeiro passo é desenhar as forças que agem sobre o pacote ao descer o plano inclinado:
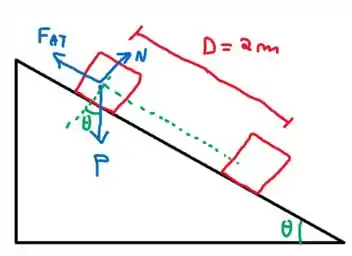
Feito isso, vamos analisar as forças atuantes no nosso sistema, usando a segunda lei de Newton, e depois calcular o trabalho de cada força lembrando que
Vamos lá!
Passo 2
Observando o diagrama, temos a força normal igual a componente vertical da força peso, ou seja:
E como , ficamos com:
Sendo assim, sabendo que a força de atrito é dada por , vamos ter:
Substituindo valores, temos:
E para a força peso:
Passo 3
Agora vamos calcular o trabalho de cada força lembrando que
Repare que o atrito faz um ângulo de com o deslocamento, de modo que
Portanto,
Passo 4
Já para a força normal, como ela é perpendicular ao deslocamento, temos que
E para o peso, vemos que o ângulo que a força faz com o deslocamento é , então:
Mas , de modo que
Passo 5
Dessa forma, o trabalho da resultante é igual a soma dos trabalhos:
Portanto,
Valeu, galera! Até a próxima! 😉