Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.1 - Ex. 1
Calcule o torque (módulo, direção e sentido) em torno de um ponto de uma força em cada uma das situações esquematizadas na Figura 10.37. Em cada caso, a força e a barra estão no plano da página, o comprimento da barra é igual a e a força possui módulo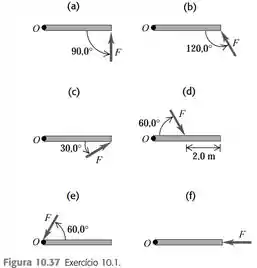 
Passo 1
Oi, galerinha! Tudo bom? Bom... o enunciado é bem direto nessa questão.
Queremos calcular o torque (módulo, direção e sentido) em torno de um ponto de uma força em cada uma das seguintes situações:
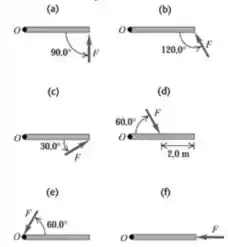
O enunciado também nos diz que a força e a barra estão no plano da página, o comprimento da barra é igual a e a força possui módulo .
Para resolvermos isso, precisamos lembrar da definição do torque:
Onde, é a força aplicada que está aparecendo em cada figura, e é o vetor que representa a distância o ponto de rotação até o ponto onde a força está sendo aplicada.
Agora vamos aplicar!! 😉
Passo 2
Veja como fica na letra a):
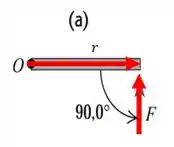
O módulo do torque da força é calculado por:
Mas a gente precisa saber a direção e sentido desse torque! Então vamos lembrar que o produto vetorial sempre resulta em um vetor perpendicular aos outros dois.
Logo, teremos que o vetor resultante para o torque terá diração sempre atravessando a tela do computador. Saindo ou entrando no plano da tela. Belezinha?
Passo 3
Para sabermos se ele está apontando pra fora ou para dentro do plano, nos podemos usar a seguinte regra:
Na fórmula o primeiro vetor é o e depois o . Veja:
Vamos colocar os dois vetores na mesma origem para facilitar a nossa visualização.
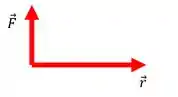
Agora colocamos o dedo indicador da mão direita apontando na mesma direção do e girá-lo em direção ao vetor , se ao fazer isso a rotação é produzida no sentido anti-horário, temos que o Torque saindo da tela, na mesma direção que estará o seu polegar.
Caso a rotação seja horária, ela produz um torque entrando na tela, como estará também seu polegar.
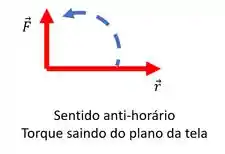
Agora que sabemos disso, vamos tentar usar o mesmo raciocínio para todos os itens. 😉
Passo 4
Letra a.
Se liga na figura:
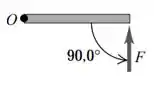
Perceba que a força está sendo aplicada em um ângulo de em relação ao eixo de rotação.
Nesse sentido, pela regra da mão direita, o sentido é para fora da página!!
Aplicando a fórmula, temos:
Utilizando os ângulos indicados na figura para achar seno, temos:
Passo 5
Letra b.
Se liga na figura:
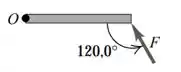
Perceba que a força está sendo aplicada em um ângulo de em relação ao eixo de rotação.
Nesse sentido, pela regra da mão direita, o sentido é para fora da página!!
Utilizando os ângulos indicados na figura para achar seno, temos:
Passo 6
Letra c.
Se liga na figura:
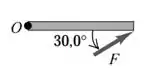
Perceba que a força está sendo aplicada em um ângulo de em relação ao eixo de rotação.
Nesse sentido, pela regra da mão direita, o sentido é para fora da página!!
Utilizando os ângulos indicados na figura para achar seno, temos:
Passo 7
Letra d.
Se liga na figura:
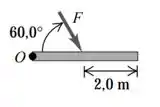
Perceba que a força está sendo aplicada em um ângulo de em relação ao eixo de rotação., mas dessa vez é do lado contrário ein!!
Além disso, a força está sendo aplicada na metada da distância total!! Assim, o tamanho do braço de alavanca vai mudar aqui hehe
Nesse sentido, pela regra da mão direita, o sentido é para dentro da página!!
Utilizando os ângulos indicados na figura para achar seno, temos:
Passo 8
Letra e.
Se liga na figura:
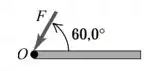
Perceba que a força está sendo aplicada em um ângulo de em relação ao eixo de rotação.
Mas aqui o tamanho do braço de alavanca é zero!!
Nesse sentido, não haverá torque!!! (imagine você abrindo uma porta pela dobradiça... difícil né haha)
Utilizando os ângulos indicados na figura para achar seno, temos:
Passo 9
Letra e.
Se liga na figura:
Perceba que a força está sendo aplicada no ângulo em relação ao eixo de rotação.
O braço de alavanca é de .
Utilizando os ângulos indicados na figura para achar seno, temos:
Ou seja, não há torque!!!