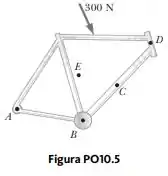
Suponha que uma única força de seja exercida no quadro de uma bicicleta, conforme mostrado na Figura PO. Considere o torque produzido por esta força em torno dos eixos perpendiculares ao plano da página e através de cada um dos pontos a , onde é o centro de massa do quadro. Classifique os torques do maior para o menor, observando que zero é maior que uma quantidade negativa. Se dois torques forem iguais, mostre esta igualdade em sua classificação.

Vem comigo que a gente resolve essa juntos!

Torque é basicamente dado por:

Onde é o ângulo entre a linha de ação da força e a linha que liga essa linha até o eixo de rotação.

Vamos traçar essas linhas na nossa imagem, temos:

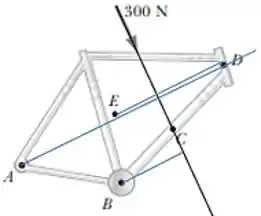
Como podemos ver todas as linhas que vão de um dos eixos até a linha de ação de força são perpendiculares a ela, menos no caso de já que alinha de ação da força passa por ele.

Então para e é igual a e para é igual a zero. Com isso já podemos ver que o torque para é zero e o que vai determinar qual torque é maior vai ser a distância entre os eixos e a linha de ação da força.