Enunciado

Física - Serway e Jewett - Física para cientistas e engenheiros - Vol1 - Ed: 1º - Capítulo 12.Perguntas Objetivas - Ex. 6

Uma prancha horizontal de 20,0 kg e 4,00 m de comprimento repousa em dois suportes, um na extremidade esquerda e outro a 1,00 m da extremidade direita. Qual é o módulo da força exercida sobre a prancha pelo suporte próximo à extremidade direita?

(a) 32,0 N (b) 45,2 N (c) 112 N (d) 131 N (e) 98,2 N.

Passo 1

O seguinte esquema ilustra mais ou menos nossa situação, olha só:

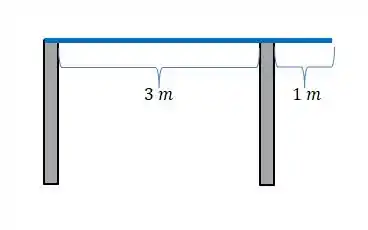
Se a gente considerar a prancha como um corpo extenso cuja massa é homogeneamente distribuída ao longo do comprimento, então o suporte da direita, que se encontra na posição vai estar a do centro de massa da prancha, que tem , na posição .

Assim, como a prancha se encontra em equilíbrio em cima dos suportes, a gente pode escrever que o torque resultante (somatório dos torques que seriam exercidos por cada suporte individualmente) é nulo.

Considerando o índice 1 pro supote da esquerda e índice 2 pro da direita, matematicamente, a gente tem:

Logo,

Onde e são as forças exercidas por cada suporte ,e e são as distâncias de cada um pro centro de massa da prancha, localizado em .

Com isso, a gente tem:

Passo 2

Analisado os torques, vamos avaliar as forças.

Você deve concordar que a prancha tem uma força peso associada à massa dela. Como ela está parada em cima dos suportes, isso significa que as forças que eles exercem sobre a prancha, somadas, precisam equivaler ao peso da prancha, não é?

Com isso, considerando , a gente tem:

Vamos substituir pela expressão que a gente obteve no último Passo, obtendo:

Multiplicando tudo por 2, a gente tem:

Por fim:

Esse então é o valor aproximado da força exercido pelo suporte da direita sobre a prancha!

Resposta

Exercícios de Livros Relacionados

A figura mostra um cilindro maciço de massa M e raio R , ao qual foi preso um segundo cilindro maciço, de massa m e raio r . Um cordão é enrolado em torno do cilindro menor. O cilindro maior está sobr

Um bastão uniforme tem comprimento L e massa M e pode girar livremente em torno de um eixo horizontal em uma de suas extremidades, como mostrado na figura. O bastão é largado do repouso em θ = θ 0 . M

Calcule o torque, em relação à origem, da força gravitacional F → = - m g j ^ que atua sobre uma partícula de massa m localizada em r → = x i ^ + y j ^ , e mostre que este torque é independente da coo

Uma força de magnitude F é aplicada horizontalmente, no sentido - x , na borda de um disco de raio R , como mostrado na figura 10-42. Escreva F → e r → em termos de vetores unitários i ^ ,j ^ e k ^ ,

Você está projetando um torno mecânico, parte de qual consiste em um cilindro uniforme de 90k g de massa e 0,40m de raio, montado de forma a girar sem atrito em torno de seu eixo. O cilindro é acionad