Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 19

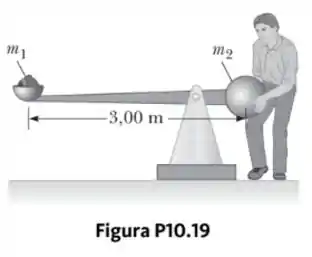
Um trabuco, ou trebuchet, foi um equipamento usado durante a Idade Média para arremessar pedras em castelos e, hoje em dia, às vezes é usado para lançar vegetais grandes e pianos como esporte. Um trabuco simples é mostrado na Figura P10.19. Modele-o como uma barra rígida de massa desprezível, 3,00   m de comprimento, unindo partículas de massa m 1   =   0,120   k g e m 2   =   60,0   k g em suas extremidades. Ele pode girar em um eixo horizontal sem atrito perpendicular à barra e a 14,0   c m da partícula de grande massa. O operador solta o trabuco do repouso no sentido horizontal.

  1. Encontre a velocidade máxima que o corpo de menor massa atinge.
  2. Enquanto o corpo de menor massa está ganhando velocidade, ele se move com aceleração constante?
  3. Ele se move com uma aceleração tangencial constante?
  4. O trabuco se move com aceleração angular constante?
  5. Ele tem um momento constante?
  6. O sistema trabuco-Terra tem energia mecânica constante?

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Letra a:

Identifique os dois objetos e a Terra como um sistema isolado. A velocidade máxima do objeto mais leve ocorrerá quando a barra estiver na posição vertical, então vamos definir o intervalo de tempo a partir de quando o sistema é liberado do repouso para quando a barra atinge uma orientação vertical. Então, para o sistema isolado,

Δ K + Δ U = 0 1 2 I 1 ω 2 + 1 2 I 2 ω 2 - 0 + m 1 g y 1 + m 2 g y 2 - 0 = 0

ω = - 2 g m 1 y 1 + m 2 y 2 I 1 + I 2 = - 2 g m 1 y 1 + m 2 y 2 m 1 r 1 2 + m 2 r 2 2

= - 2 9.80 m s 2 [ ( 0.120 k g ) ( 2.86 m ) + ( 60.0 k g ) ( - 0.140 m ) ( 0.120 k g ) ( 2.86 m ) 2 + ( 60.0 k g ) ( 0.140 m ) 2

= 8.55 r a d s

Então, a velocidade tangencial do objeto mais leve é:

v = r ω = 2.86 m 8.55 r a d s = 24.5 m s

Passo 2

Letra b:

Não. A aceleração geral não é constante. Tem que se mover também em uma linha reta ou caminho parabólico para ter uma chance de estar sob aceleração constante. O caminho circular apresentado aqui descarta essa possibilidade.

Passo 3

Letra c:

Não. Ele se move com aceleração tangencial constante, pois a aceleração angular não é constante. Veja a explicação na parte (d).

Passo 4

Letra d:

Não. O braço de alavanca da força gravitacional atuando na massa de 60 kg muda durante o movimento. Como resultado, o torque muda, e o mesmo acontece com a aceleração angular.

Passo 5

Letra e:

Não. A velocidade angular muda, portanto o momento angular do trabuco muda.

Passo 6

Letra f:

Sim. A energia mecânica permanece constante porque o sistema é isolado - é assim que resolvemos o problema em (a).

Resposta

  1. 24.5 m s
  2. N ã o
  3. Não
  4. Não
  5. Não
  6. Sim
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para construir uma escultura móvel, um artista pendura uma esfera de alumínio de 6,0 kg de massa presa a um fio de aço da 0,50 m de comprimento com área da seção reta igual a 2,5 × 10 - 3c m . À parte
Calcule a magnitude da força F horizontal que é preciso aplicar, em direção ao eixo O , para conseguir que um tambor cilíndrico, de massa M e raio R , suba um degrau de altura dR (Fig.)
Na Fig. 10-39, um cilindro com uma massa de 2,0 kg pode girar em torno do eixo central, que passa pelo ponto O. As forças mostradas têm os seguintes módulos: F 1 = 6,0N ,F 2 =4,0N , F 3 = 2,0NeF 4 = 5
Calcule (a) o torque, (b) a energia e (c) a potência média necessária para acelerar a Terra em 1 dia desde o repouso até sua velocidade angular atual em relação ao eixo de rotação,
Até hoje se discute de que forma os pesados lintéis (blocos horizontais de pedra) foram colocados sobre blocos verticais em Stonehenge. Um possível método foi testado em uma pequena cidade tcheca. Um