Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Perguntas Objetivas - Ex. 16
Uma barra de 7,0 m de comprimento é articulada em um ponto a 2,0 m da extremidade esquerda. Uma força para baixo de 50 N age sobre a extremidade esquerda, e outra de 200 N, sobre a extremidade direita. A que distância à direita da articulação uma terceira força de 30 N para cima pode ser colocada para produzir equilíbrio rotacional? Observação: Ignore o peso da barra.
(a) 1,0 m (b) 2,0 m (c) 3,0 m (d) 4,0 m (e) 3,5 m.
Passo 1
Vamos começar com um esqueminha da situação pra gente visualizar tudo melhor. Olha só:
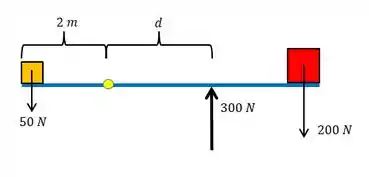
Aqui então a gente vai tentar descobrir a distância entre os dois pontos de apoio da barra.
Vamos estabelecer o seguinte: pra barra estar em equilíbrio rotacional, os torques que agem à esquerda da articulação precisam equivaler matematicamente aos que agem à direita da mesma.
Escrevendo matematicamente o que acabamos de estabelecer:
Onde e são os torques dos pesos nas extremidades, e é o torque de . Certinho até aqui?
Passo 2
Agora, vamos aplicar a formulinha pro torque pra cada peso e cada ponto de apoio a partir dessa equaçãozinha. Vamos ter o seguinte:
Aqui a força leva sinal negativo uma vez que tem sentido contrário à força do peso da extremidade direita. Isso é uma convenção pra esse exercício!
Uma legendinha ajuda! Aqui, temos:
e como as forças que cada peso de cada extremidade faz pra baixo; , ;
e como as distâncias de cada peso à articulação; , ;
Aplicando os dados que a gente tem, ficamos com o seguinte:
Desenvolvendo isso, a gente vai ter:
Resposta
.