Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 22.Problemas - Ex. 35
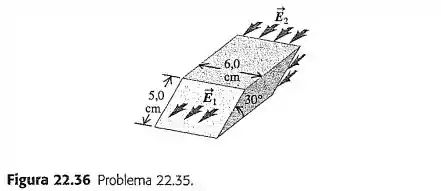
O campo elétrico em uma das faces de um paralelepípedo é uniforme em todos os pontos dessa face e aponta perpendicularmente para fora da face. Na face oposta, o campo elétrico também é uniforme em todos os pontos e aponta perpendicularmente para dentro da face (Figura ). As duas faces mencionadas possuem uma inclinação de em relação à horizontal, enquanto e são, ambos, horizontais; o módulo de é igual a e o módulo de é igual a . Supondo que nenhuma outra linha de campo atravesse as superfícies do paralelepípedo, determine a carga líquida contida em seu interior. O campo elétrico existente é produzido somente pelas cargas no interior do paralelepípedo ou pode ser produzido também por cargas existentes fora dele? Como se pode ter certeza disso?
Passo 1
O cálculo da carga total no interior do paralelepípedo pode ser dado através da lei de Gauss, que é dada por:
Ou:
Então, a carga total pode ser relacionada com o fluxo elétrico total resultante da soma dos fluxos de cada campo elétrico.
Devemos lembrar também que, o campo elétrico é positivo quando está “saindo” de uma superfície e é negativo quando ocorre o contrário.
Passo 2
Logo, teremos que:
Onde a área é dada por:
E, substituindo os valores:
Portanto:
Passo 3
Como o fluxo elétrico no interior do paralelepípedo não é nulo, isso significa que existem cargas em seu interior também. Mas isso não significa que elas são as únicas presentes.
Visto que o campo elétrico vai para a parte externa da face do corpo geométrico, deve haver cargas externas ao corpo. Caso contrário, o campo elétrico estará limitado apenas à superfície da face.
Resposta
Não