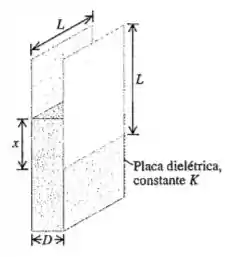
Duas placas condutoras quadradas, cada qual com lado igual a , são separadas por uma distancia D. Uma placa dielétrica, com constante dielétrica K e com dimensões , é inserida até uma distância x no espaço entre as placas, como indicado na figura 24.41. (a)Calcule a capacitância do sistema (Veja o problema 24.72) (b)Suponha que o capacitor seja conectado a uma bateria que mantém uma diferença de potencial constante V entre as placas. Se a placa dielétrica for inserida até uma distância adicional dx no espaço entre as placas, mostre que a variação de energia acumulada é dada por:
(c)Suponha que, antes de a placa se mover a uma distância dx, as placas sejam desconectadas da bateria, de modo que as cargas das placas permanecem constantes. Determine o módulo da carga em cada placa e, a seguir, mostre que, quando a placa penetra mais uma distancia dx no interior do espaço entre as placas, a energia acumulada varia de uma quantidade igual módulo, mas de sinal contrário ao valor de , encontrado no item (b). (d) Se F for o módulo da força exercida sobre o dielétrico pelas cargas das placas, então deve ser igual ao trabalho realizado contra essa força para deslocar o diel´petrico até uma distância . Portanto, . Mostre que a aplicação desse resultado na parte (b) fornece uma resposta incorreta para o sentido dessa força. (Esse método não exige o conhecimento do campo nas bordas do capacitor.)
Passo 1
O sistema pode ser considerado por dois capacitores em pararelo, uma com área e o ar entre as placas e uma com área e o preenchimento feito pelo dielétrico. Temos que:
Logo (a),
![]()
Passo 2
Para (b) temos que:
![]()
Onde,
![]()
Com
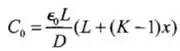
Isso nos dá:
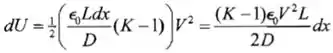
Passo 3
(c)Se a carga é mantida constante entre as placas, temos que:
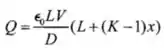
E,

Portanto,
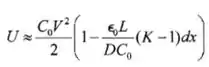
Logo,
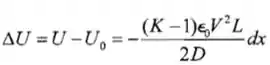
(d) Como
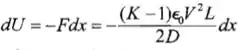
A força está na direção oposta do movimento dx, significando que a placa sente uma força empurrando!
(e) Quando as placas estão conectadas na bateria, as placas mais a laje não são um sistema isolado. Logo, comparando os resultados com (c), temos que:
![]()