Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Problemas - Ex. 59

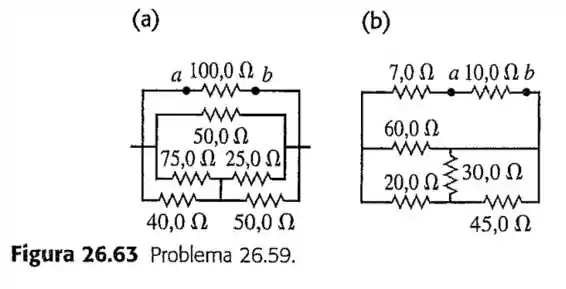
59- Caso um ohmímetro seja conectado entre os pontos e em cada circuito indicado na Figura , qual será a sua leitura?

Passo 1

Não teremos uma leitura de resistência de na letra e de na letra , pois além desses resistores tem todo o circuito em volta dele saca? Para ficar claro vamos redesenhar a letra e ir com calma.

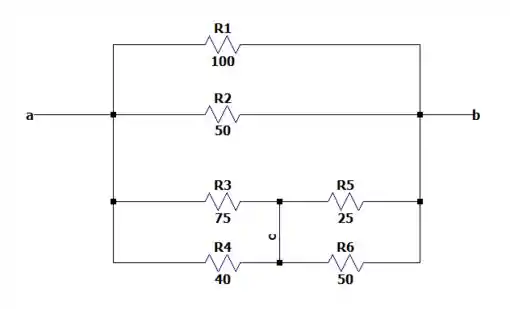
Pois toda a parte esquerda do circuito tem tensão igual a e a direita igual a , então o circuito pode ser redesenhado da forma acima.

Onde os resistores de e de estão em paralelo e terão uma resistência equivalente de:

E a linha tem o mesmo potencial elétrico, durante todo o seu comprimento, portanto os resistores de e de estão em paralelo (conectado entre os pontos e ) e os resistores de e de também estão em paralelo (conectados entre os pontos e ). Nos dando resistências iguais a:

Passo 2

Então o circuito fica da seguinte forma:

Podemos ver que as resistências de e de estão em série e a equivalência entre eles está em paralelo com o resistor de , então a resistência equivalente entre e será:

Passo 3

Aplicando mais ou menos o mesmo raciocínio na letra nós teremos o seguinte desenho redesenhado:

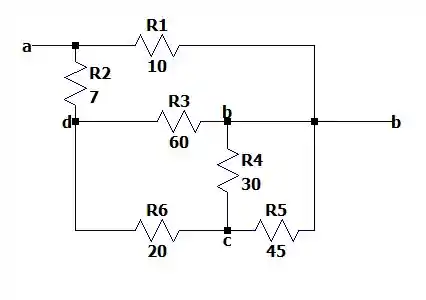
Bem, esse circuito não dá para fazer muito milagre, mas anotando os pontos que tem mesmo potencial podemos ver que o resistor de e de estão em paralelo pois estão ligados em e em e valem:

O que deixa nosso circuito da seguinte forma:

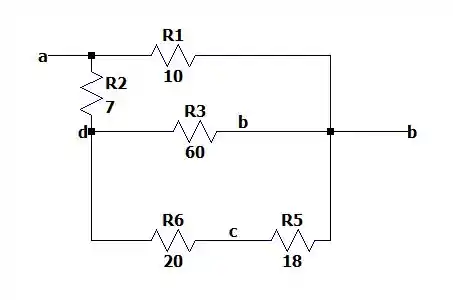
E com isso vemos que o resistor de está em paralelo com os resistores em série de e de e que nos dará um resistor equivalente de:

Passo 4

Então o circuito equivalente fica como:

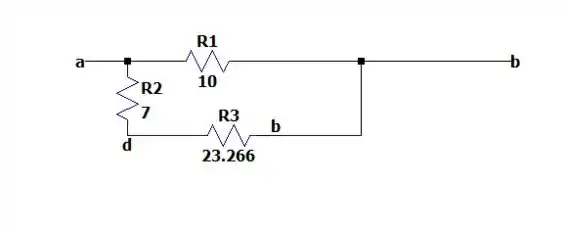
Então note que os resistores de e de estão em série formando uma linha que vai de até e será um resistor equivalente de e esse resistor equivalente (que está conectado entre e )está em paralelo com o resistor de e que dará um resistor equivalente entre e igual a:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 27-52, um conjunto de n resistores em paralelo é ligado em série a um resistor e a uma fonte ideal. Todos os resistores têm a mesma resistência. Se um outro resistor de mesmo valor fosse ligad

A Fig. 27-49 mostra uma parte de um circuito. As resistências são R 1 = 2,0 Ω , R 2 = 4,0 Ω e R 3 = 6,0 Ω e a corrente indicada é i = 6,0 A . A diferença de potencial entre os pontos A e B que ligam o

Duas fontes iguais de força eletromotriz ε = 12,0 V e resistencia interna r = 0,200 Ω podem ser ligadas a uma resistência R em paralelo (Fig. 27-50) ou em série (Fig. 27-51). Se R = 2,00 r , é a corre

Na Fig. 27-44, a corrente na resistência 6 é i 6 = 1,40 A e as resistências são R 1 = R 2 = R 3 = 2,00 Ω , R 4 = 16,0 Ω , R 5 = 8,00 Ω e R 6 = 4,00 Ω . Qual é a força eletromotriz da fonte ideal?

Na Fig. 27-46, ε = 12,0 V , R 1 = 2000 Ω , R 2 = 3000 Ω e R 3 = 4000 Ω . Determine as diferenças de potencial (a) V A - V B ; (b) V B - V C (c) V C - V D ; (d) V A - V C .