Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 30.Exercício - Ex. 30
30- Um capacitor de é conectado a uma bateria de por alguns segundos e, a seguir, conectado a um indutor de com resistência desprezível.
Após o capacitor e o indutor estarem ambos conectados, determine a corrente máxima no circuito. Quando a corrente é máxima, qual é a carga no capacitor?
Quanto tempo após o capacitor e o indutor serem conectados em conjunto o capacitor é completamente descarregado da primeira vez? E da segunda vez?
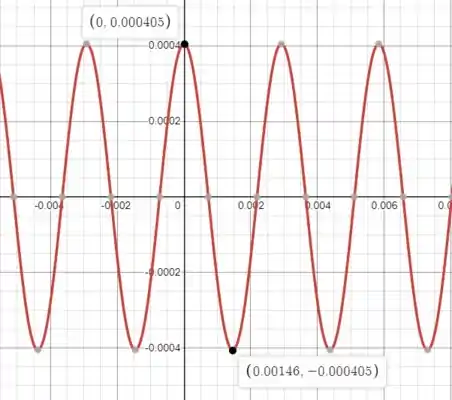
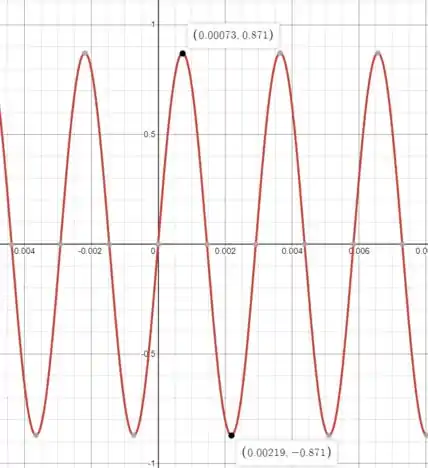
Faça gráficos da carga nas placas do capacitor e da corrente que passa pelo indutor em função do tempo?
Passo 1
A corrente máxima em um circuito é dado por:
Pois é quando
Onde é dado por:
E será:
Então a corrente será de:
E quando a corrente é máxima não existe nenhuma carga no capacitor, pois tudo está no indutor.
O valor da carga é de e
Passo 2
Na letra nós precisamos saber o período de oscilação desse circuito e que será dado por:
Como anotamos o valor de no final do passo anterior nós teremos que o período será de:
E da figura da quinta edição desse livro vemos que a carga no capacitor é zerada em então a primeira vez que ele se descarrega será em:
E a segunda vez será em:
Passo 3
O gráfico da corrente será dado por:
E será:
Já a equação da carga será de:
