Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 49
Um capacitor esférico consiste em uma fina casca esférica de raio e de uma fina casca esférica concêntrica de raio , onde .
(a) Mostre que a capacitância é dada por .
(b) Mostre que, quando os raios das cascas são praticamente iguais, a capacitância é aproximadamente dada pela expressão para a capacitância de um capacitor de placas paralelas, , onde é a área da esfera e .
Passo 1
Acho que a primeira coisa a se fazer aqui é desenhar essas duas cascas esféricas concêntricas, não é verdade?
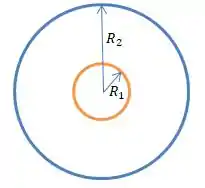
Então, para demonstrar o valor da capacitância, vamos supor que exista uma carga na esfera laranja e uma carga na esfera de raio azul. Beleza?
Passo 2
De acordo com a teoria, para uma esfera condutora carregada de carga , o potencial são esferas concêntricas...
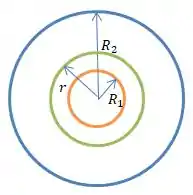
E varia com o raio ...
Então, a diferença de potencial entre as esferas laranja e azul será...
Então...
Passo 3
Então, agora que conhecemos a diferença de potencial entre as esferas, basta se lembrar de que a capacitância pode ser determinada a partir de...
Então...
Passo 4
Veja que quando , ou seja, a esfera laranja quase se coincide com a esfera azul, podemos falar que...
Só que o que é ?
É a área da esfera de raio ...
Onde (é a largura de separação entre as esferas).
Resposta
Letra A:
Letra B: